题目内容
如图，P1，P2，P3是双曲线上的三点，过这三点分别作y的垂线，得到三个△P1A1O，△P2A2O，△P3A3O，设它们的轴面积分别为S1，S2，S3，则S1，S2，S3的大小关系是（ ）| A、S1=S2=S3 | B、S1=S3＜S2 | C、S2＞S3＞S1 | D、无法确定 |
分析：过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S=
|k|．
| 1 |
| 2 |
解答：解：由题意得：直角三角形面积S是个定值，即S=
|k|．
所以S1=S2=S3．
故选A．
| 1 |
| 2 |
所以S1=S2=S3．
故选A．
点评：主要考查了反比例函数y=
中k的几何意义，即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
|k|．
| k |
| x |
| 1 |
| 2 |
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
22、如图，P1、P2…P5是平行四边形ABCD的对角线BD的6等分点．请以图中的点为顶点重新画出一个平行四边形，并说明理由．
如图，P1、P2、P3是双曲线上的三点，过这三点分别作y轴的垂线，得到三个三角形P1A1O、P2A2O、P3A3O，设它们的面积分别是S1、S2、S3，则S1、S2、S3的大小关系为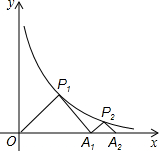
（2011•峨眉山市二模）如图，P1、P2是函数
（2012•柳州）如图，P1、P2、P3这三个点中，在第二象限内的有（ ）