题目内容
在图中，图①是一个扇形AOB，将其作如下划分．C第一次划分：如图②所示，以OA的一半OA1为半径画弧，再作∠AOB的平分线，得到扇形的总个数为6个，第二次划分：如图③所示，在扇形C1OB1中，按上述划分方式继续划分，可以得到扇形的总数为11个； 第三次划分：如图④所示，依次划分下去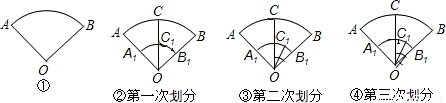
（1）根据题意完成下表：
| 划分次数 | 扇形总数 |
| 1 | 6 |
| 2 | 11 |
| 3 | |
| 5 | |
| ????? | ??? |
| n |
【答案】分析：（1）通过划分条件，每划分一次，就增加5个扇形，根据此可得到规律，完成上表．
（2）设划分n次时，得到扇形2009个，求出n为整数时就存在，不是整数时就不存在．
解答：解：（1）划分一次时，为1+5=6，
划分两次时，为1+5×2=11，
划分三次时，为1+5×3=16，
划分5次时，为1+5×5=26．
划分n次时，为1+5n次．
故答案为：16，26，1+5n；
（2）设划分n次时，得到扇形2009个，
1+5n=2009，
n=401.6，
故n不是整数，不能划分成2009个扇形．
点评：本题考查理解题意的能力，是个规律性题目，关键找到规律，写出一般式，第二问把2009和一般式联系起来列成方程，可求解．
（2）设划分n次时，得到扇形2009个，求出n为整数时就存在，不是整数时就不存在．
解答：解：（1）划分一次时，为1+5=6，
划分两次时，为1+5×2=11，
划分三次时，为1+5×3=16，
划分5次时，为1+5×5=26．
划分n次时，为1+5n次．
故答案为：16，26，1+5n；
（2）设划分n次时，得到扇形2009个，
1+5n=2009，
n=401.6，
故n不是整数，不能划分成2009个扇形．
点评：本题考查理解题意的能力，是个规律性题目，关键找到规律，写出一般式，第二问把2009和一般式联系起来列成方程，可求解．
练习册系列答案
阅读快车系列答案
相关题目
角和半径．
（体验探究题）阅读下列解题过程并填空．
