题目内容
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。
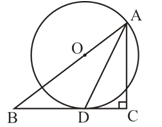
(1)求证:BC是⊙O切线;
(2)若BD=5, DC=3,求AC的长。
【答案】(1)见解析证明;(2)见解析证明.
【解析】
试题分析:(1)要证BC是⊙O的切线,只要连接OD,再证OD⊥BC即可;(2)过点D作DE⊥AB,根据角平分线的性质可知CD=DE=3,由勾股定理得到BE的长,再通过证明△BDE∽△BAC,根据相似三角形的性质得出AC的长.
试题解析:(1)证明: 如图1,连接OD.∵ OA=OD, AD平分∠BAC,∴ ∠ODA=∠OAD, ∠OAD=∠CAD,∴ ∠ODA=∠CAD,∴ OD//AC,∴ ∠ODB=∠C=90,∴ BC是⊙O的切线;

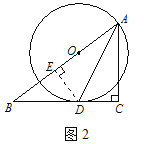
(2) 如图2,过D作DE⊥AB于E.∴ ∠AED=∠C=90,又∵ AD=AD, ∠EAD=∠CAD, ∴ △AED≌△ACD.
∴ AE=AC, DE=DC=3,在Rt△BED中,∠BED =90,由勾股定理,得BE=![]() .设AC=x(x>0), 则AE=x,在Rt△ABC中,∠C=90, BC=BD+DC=8, AB=x+4, 由勾股定理,得
.设AC=x(x>0), 则AE=x,在Rt△ABC中,∠C=90, BC=BD+DC=8, AB=x+4, 由勾股定理,得![]() ,
,
解得x=6,即 AC=6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】春节将至,某移动公司计划推出两种新的计费方式,如下表所示:
方式1 | 方式2 | |
月租费 | 30元/月 | 0 |
本地通话费 | 0.20元/分钟 | 0.40元/分钟 |
请解决以下两个问题:(通话时间为正整数)
(1)若本地通话100分钟,按方式一需交费多少元?按方式二需交费多少元?
(2)对于某月本地通话,当通话多长时间时,按两种计费方式的收费一样多?