题目内容
如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:EC=BF.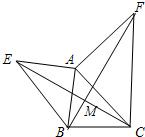
分析:首先根据角间的关系推出∠EAC=∠BAF.再根据边角边定理,证明△EAC≌△BAF.最后根据全等三角形的性质定理,得知EC=BF.
解答:证明:∵AE⊥AB,AF⊥AC?∠EAB=90°=∠FAC?∠EAB+∠BAC=∠FAC+∠BAC
又∵∠EAC=∠EAB+∠BAC,∠BAF=∠FAC+∠BAC
∴∠EAC=∠BAF
在△EAC与△BAF中,
?△EAC≌△BAF(SAS)
∴EC=BF
又∵∠EAC=∠EAB+∠BAC,∠BAF=∠FAC+∠BAC
∴∠EAC=∠BAF
在△EAC与△BAF中,
|
∴EC=BF
点评:本题考查全等三角形的判定与性质定理.解决本题需要同学们对全等三角形的性质与判定要全面掌握,并做到灵活运用的能力.

练习册系列答案
相关题目
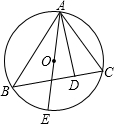 如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高.
如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高.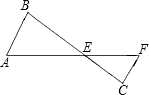 如图所示,已知AE=54,BE=45,FE=36,CE=30,CF=26.
如图所示,已知AE=54,BE=45,FE=36,CE=30,CF=26.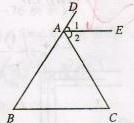 24、如图所示,已知AE∥BC,∠B=∠C.
24、如图所示,已知AE∥BC,∠B=∠C.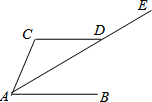 (2013•宜春模拟)如图所示,已知AE平分∠BAC交CD于点D,且AB∥CD,∠C=100°,则∠EAC为( )
(2013•宜春模拟)如图所示,已知AE平分∠BAC交CD于点D,且AB∥CD,∠C=100°,则∠EAC为( )