题目内容
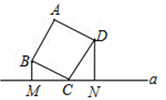
已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E,联结AC、DF,∠A=∠D.
求证:AB=DE.
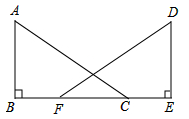
求证:AB=DE.

证明见解析.
试题分析:由条件先得出BC=EF和∠B=∠E,再根据角角边就可以判断△ABC≌△DEF,利用全等三角形的性质即可证明:AB=DE.
试题解析:∵BF=CE,
∴BF+CF=CE+CF,即BC=EF.
∵AB⊥BE,DE⊥BE,∴∠B=∠E=90°.
在△ABC和△DEF中,AB=DE,∠B=∠E,∠A=∠D,
∴△ABC≌△DEF(SAS),
∴AB=DE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
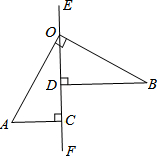
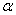 .
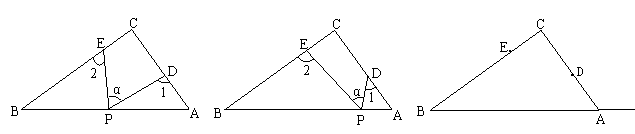
.



 , 则
, 则 的度数等于( )
的度数等于( )




