ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌШєЕуPЕФзјБъЮЊ![]() ,дђЖЈвхЃК
,дђЖЈвхЃК ![]() ЮЊЕуPЕНзјБъдЕуOЕФЁАелЯпОрРыЁБ.
ЮЊЕуPЕНзјБъдЕуOЕФЁАелЯпОрРыЁБ.
ЃЈ1ЃЉШєвбжЊPЃЈ-2ЃЌ3ЃЉЃЌдђЕуPЕНзјБъдЕуOЕФЁАелЯпОрРыЁБdЃЈ-2ЃЌ3ЃЉ= ЃЛ
ЃЈ2ЃЉШєЕуPЃЈxЃЌyЃЉТњзу2x+y=0,ЧвЕуPЕНзјБъдЕуOЕФЁАелЯпОрРыЁБdЃЈxЃЌyЃЉ=6ЃЌЧѓГіPЕФзјБъЃЛ
ЃЈ3ЃЉШєЕуPЕНзјБъдЕуOЕФЁАелЯпОрРыЁБdЃЈxЃЌyЃЉ=3ЃЌЪддкзјБъЯЕФкЛГіЫљгаТњзуЬѕМўЕФЕуPЙЙГЩЕФЭМаЮЃЌВЂЧѓГіИУЭМаЮЕФЫљЮЇГЩЗтБеЧјгђЕФУцЛ§.

ЁОД№АИЁПЃЈ1ЃЉ5ЃЛЃЈ2ЃЉЃЈ2ЃЌ-4ЃЉЃЌЃЈ-2,4ЃЉЃЌЃЈ6ЃЌ-12ЃЉЛђЃЈ-6,12ЃЉЃЛЃЈ3ЃЉЛЭММћНтЮіЃЌУцЛ§ЮЊ18.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЖЈвхЧѓГіМДПЩЃЛЃЈ2ЃЉгЩdЃЈxЃЌyЃЉ=![]() =6ЃЌдйгЩ2x+y=0СНЪНЧѓГіxЁЂyЃЛЃЈ3ЃЉгЩdЃЈxЃЌyЃЉ=
=6ЃЌдйгЩ2x+y=0СНЪНЧѓГіxЁЂyЃЛЃЈ3ЃЉгЩdЃЈxЃЌyЃЉ=![]() =3ЃЌЕУГіЂйy=-x+3ЃЛЂкy=x-3ЃЛЂлy=x+3ЃЛЂмy=-x-3.ЗжБ№ЛГіЫФЬѕжБЯпЃЌдйЧѓЮЇГЩУцЛ§.
=3ЃЌЕУГіЂйy=-x+3ЃЛЂкy=x-3ЃЛЂлy=x+3ЃЛЂмy=-x-3.ЗжБ№ЛГіЫФЬѕжБЯпЃЌдйЧѓЮЇГЩУцЛ§.
НтЃКЃЈ1ЃЉdЃЈ-2ЃЌ3ЃЉ=![]() =5ЃЛ
=5ЃЛ
ЃЈ2ЃЉгЩdЃЈxЃЌyЃЉ=![]() =6ЃЌгж2x+y=0ЃЌдђЂй
=6ЃЌгж2x+y=0ЃЌдђЂй![]() НтЕУ
НтЕУ![]() Ђк
Ђк![]() НтЕУ
НтЕУ![]() Ђл
Ђл![]() НтЕУ
НтЕУ![]() Ђм
Ђм![]() НтЕУ
НтЕУ![]() дђЕуPзјБъЮЊЃЈ2ЃЌ-4ЃЉЁЂЃЈ-2,4ЃЉЁЂЃЈ6ЃЌ-12ЃЉЛђЃЈ-6,12ЃЉЃЛ
дђЕуPзјБъЮЊЃЈ2ЃЌ-4ЃЉЁЂЃЈ-2,4ЃЉЁЂЃЈ6ЃЌ-12ЃЉЛђЃЈ-6,12ЃЉЃЛ
ЃЈ3ЃЉгЩdЃЈxЃЌyЃЉ=![]() =3ЃЌдђЂйx+y=3,ЕУy=-x+3ЃЛЂкx-y=3ЃЌЕУy=x-3ЃЛЂл-x+y=3ЃЌЕУy=x+3ЃЛЂм-x-y=3ЃЌЕУy=-x-3.
=3ЃЌдђЂйx+y=3,ЕУy=-x+3ЃЛЂкx-y=3ЃЌЕУy=x-3ЃЛЂл-x+y=3ЃЌЕУy=x+3ЃЛЂм-x-y=3ЃЌЕУy=-x-3.
ЛГіЭМЯѓЮЊ
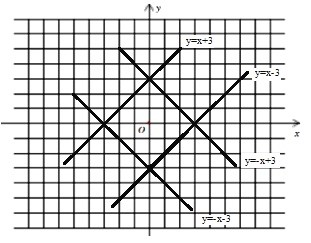
ЮЇГЩЧјгђУцЛ§ЮЊ4ЁС![]() ЁС3ЁС3=18.
ЁС3ЁС3=18.




