题目内容
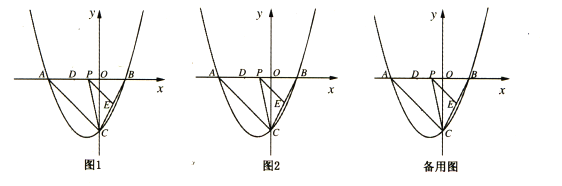
【题目】如图,抛物线![]() 与y轴交于点C(0,-4),与x轴交于点A、B,且B点的坐标为(2,0).
与y轴交于点C(0,-4),与x轴交于点A、B,且B点的坐标为(2,0).
(1)求抛物线的解析式;
(2)若点P是AB上的一个动点,过点P作PE∥AC交BC于点E,连接CP,求△PCE面积最大时P点的坐标;
(3)在(2)的条件下,若点D为OA的中点,点M是线段AC上一点,当△OMD为等腰三角形时,连接MP、ME,把△MPE沿着PE翻折,点M的对应点为点N,直接写出点N的坐标.
【答案】(1)抛物线的解析式为y=![]() 4;
4;
(2) 当P点的坐标为(-1,0)时, S△PCE的最大,且最大值为3;
(3) M点关于PE的对称点N的坐标为(1,1)或(2,0).
【解析】(1)利用待定系数法求出抛物线的解析式;(2)首先求出△PCE面积的表达式,然后利用二次函数的性质求出其最大值;(3)△OMD为等腰三角形,可能有三种情形,需要分类讨论.
解:(1)把点C(0,﹣4),B(2,0)分别代入y=![]() x2+bx+c中,
x2+bx+c中,
得 ,
,
解得![]()
∴该抛物线的解析式为y=![]() x2+x﹣4.
x2+x﹣4.
(2)令y=0,即![]() x2+x﹣4=0,解得x1=﹣4,x2=2,
x2+x﹣4=0,解得x1=﹣4,x2=2,
∴A(﹣4,0),S△ABC=![]() ABOC=12.
ABOC=12.
设P点坐标为(x,0),则PB=2﹣x.
∵PE∥AC,
∴∠BPE=∠BAC,∠BEP=∠BCA,
∴△PBE∽△ABC,
∴![]() ,即
,即![]() ,
,
化简得:S△PBE=![]() (2﹣x)2.
(2﹣x)2.
S△PCE=S△PCB﹣S△PBE=![]() PBOC﹣S△PBE=
PBOC﹣S△PBE=![]() ×(2﹣x)×4﹣
×(2﹣x)×4﹣![]() (2﹣x)2
(2﹣x)2
=![]() x2﹣
x2﹣![]() x+
x+![]()
=![]() (x+1)2+3
(x+1)2+3
∴当x=﹣1时,S△PCE的最大值为3.
(3)△OMD为等腰三角形,可能有三种情形:(I)当DM=DO时,如答图①所示.
DO=DM=DA=2,
∴∠OAC=∠AMD=45°,
∴∠ADM=90°,
∴M点的坐标为(﹣2,﹣2);

(II)当MD=MO时,如答图②所示.
过点M作MN⊥OD于点N,则点N为OD的中点,
∴DN=ON=1,AN=AD+DN=3,
又△AMN为等腰直角三角形,∴MN=AN=3,
∴M点的坐标为(﹣1,﹣3);
(III)当OD=OM时,
∵△OAC为等腰直角三角形,
∴点O到AC的距离为![]() ×4=
×4=![]() ,即AC上的点与点O之间的最小距离为
,即AC上的点与点O之间的最小距离为![]() .
.
∵![]() >2,∴OD=OM的情况不存在.
>2,∴OD=OM的情况不存在.
综上所述,点M的坐标为(﹣2,﹣2)或(﹣1,﹣3).

“点睛”本题是二次函数综合题,考查了二次函数的图象与性质、待定系数法、相似三角形、等腰三角形等知识点,以及分类讨论的数学思想.第(2)问将面积的最值转化为二次函数的极值问题,注意其中求面积表达式的方法;第(3)问重在考查分类讨论的数学思想,注意三种可能的情形需要一一分析,不能遗漏.