题目内容
【题目】如图,已知△ABC中,AB=AC,利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法),并根据要求填空:
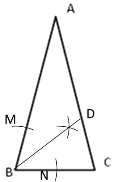
(1)作∠B的平分线BD,交AC于点D;
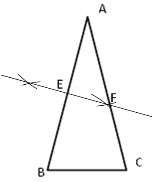
(2)作线段AB的垂直平分线EF,交AB于点E,交AC于点F;
(3)如果点F与点D重合,则∠A= °.

【答案】(1)见解析;(2)见解析;(3)36°
【解析】
(1)以B为圆心,以任意长度为半径作弧,分别交AB、BC与M、N,分别以M、N为圆心,以大于![]() MN为半径作弧,连接B和两弧的交点并延长交AC于D,BD即为所求;
MN为半径作弧,连接B和两弧的交点并延长交AC于D,BD即为所求;
(2)分别以A、B为圆心,以大于![]() AB为半径作弧,连接两弧的两个交点交AB于E,交AC于F,EF即为所求;
AB为半径作弧,连接两弧的两个交点交AB于E,交AC于F,EF即为所求;
(3)根据等边对等角可得:∠ABC=∠ACB,再根据角平分线的定义可得:∠ABC=2∠ABF,然后根据垂直平分线的性质和等边对等角可得:∠FBA=∠A,从而得出∠ACB=∠ABC=2∠A,最后根据三角形的内角和定理列方程即可求出∠A.
解:(1)以B为圆心,以任意长度为半径作弧,分别交AB、BC与M、N,分别以M、N为圆心,以大于![]() MN为半径作弧,连接B和两弧的交点并延长交AC于D,如下图所示,BD即为所求;
MN为半径作弧,连接B和两弧的交点并延长交AC于D,如下图所示,BD即为所求;
(2)分别以A、B为圆心,以大于![]() AB为半径作弧,连接两弧的两个交点交AB于E,交AC于F,如下图所示EF即为所求;
AB为半径作弧,连接两弧的两个交点交AB于E,交AC于F,如下图所示EF即为所求;
(3)当F、D重合时,如下图所示,
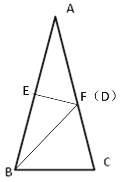
∵AB=AC
∴∠ABC=∠ACB
∵BF平分∠ABC
∴∠ABC=2∠ABF
∵EF垂直平分AB
∴FB=FA
∴∠FBA=∠A
∴∠ACB=∠ABC=2∠A
∵∠ACB+∠ABC+∠A=180°
∴2∠A+2∠A+∠A=180°
解得:∠A=36°

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目