题目内容
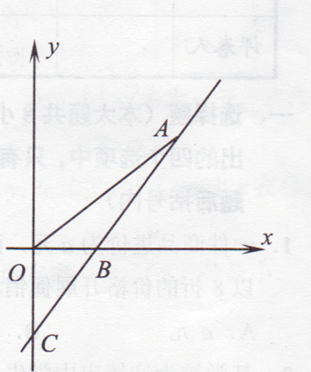
【题目】如图,直线y=kx-3与x轴、y轴分别交于点B,C, ![]() =
= ![]() .
.
(1)求点B坐标和k值;
(2)若点A(x,y)是直线y=kx-3上在第一象限内的一个动点,当点A在运动过程中,试写出△AOB的面积S与x的函数关系式(不要求写自变量范围);并进一步求出点A的坐标为多少时,△AOB的面积为 ![]() ?
?
(3)在上述条件下,x轴上是否存在点P,使△AOP为等腰三角形?若存在,请写出满足条件的所有P点坐标;若不存在,请说明理由.
【答案】
(1)
(1)∵直线y=kx-3与y轴的交点为C(0,-3)
∴OC=3
∵ ![]() =
= ![]()
∴OB= ![]()
∴B点坐标为( ![]() ,0)
,0)
将B( ![]() ,0)代入y=kx-3,得
,0)代入y=kx-3,得
![]() k-1=0
k-1=0
解得k=2.
(2)
解:由(1)可知直线的解析式是y=2x-3,
S= ![]() ×OB×yA
×OB×yA
= ![]() ×
× ![]() ×(2x-3)
×(2x-3)
= ![]() x-
x- ![]()
即:三角形AOB的面积S与x的函数关系式为S= ![]() x-
x- ![]() ,
,
当S= ![]() 时,
时, ![]() x-
x- ![]() =
= ![]() ,解得x=3,则2x-3=3,即A(3,3).
,解得x=3,则2x-3=3,即A(3,3).
所以当点A的坐标为(3,3)时,△AOB的面积为 ![]() ?
?
(3)
解:存在.由(2)得A(3,3),AO=3 ![]() ,∠AOB=45°,
,∠AOB=45°,
当OP=AO=3 ![]() 时,P(3
时,P(3 ![]() ,0)或P(-3
,0)或P(-3 ![]() ,0);
,0);
当AP=OA=3 ![]() 时,∠APO=∠AOP=45°,则OP=
时,∠APO=∠AOP=45°,则OP= ![]() OA=6,P(6,0);
OA=6,P(6,0);
当OP=AP时,P(3,0).
【解析】(1)当x=0时,y=-3,即C(0,-3),由 ![]() =
= ![]() 求出B点坐标,将它代入直线y=kx-3可求出k;(2)因为点A在直线y=2x-3上,则A(x, 2x-3),由S=
求出B点坐标,将它代入直线y=kx-3可求出k;(2)因为点A在直线y=2x-3上,则A(x, 2x-3),由S= ![]() ×OB×yA , 代入相应值即可求出S关于x的函数关系式;令S=
×OB×yA , 代入相应值即可求出S关于x的函数关系式;令S= ![]() 时,求出x的值,并代入直线解析式求出A点的坐标;(3)分类讨论:当OP=AO时,当AP=OA时,当OP=AP时.结合A(3,3),AO=3
时,求出x的值,并代入直线解析式求出A点的坐标;(3)分类讨论:当OP=AO时,当AP=OA时,当OP=AP时.结合A(3,3),AO=3 ![]() ,∠AOB=45°解题即可.
,∠AOB=45°解题即可.
【考点精析】本题主要考查了一次函数的性质和一次函数的图象和性质的相关知识点,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能正确解答此题.

【题目】为了解某县2011年初中毕业生的实验考查成绩等级的分布情况,随机抽取了该县若干名学生的实验考查成绩进行统计分析,并根据抽取的成绩绘制了如下的统计图表:
成绩等级 | A | B | C | D |
人数 | 60 | x | y | 10 |
百分比 | 30% | 50% | 15% | m |
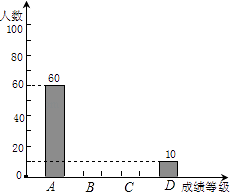
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有名;
(2)表中x,y和m所表示的数分别为:x= , y= , m=;
(3)请补全条形统计图;
(4)根据抽样调查结果,请你估计2011年该县5400名初中毕业生实验考查成绩为D类的学生人数.