题目内容
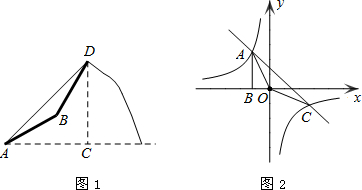
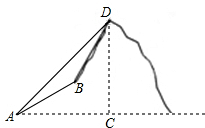 由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°.
由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°.(1)求线段BD的长;
(2)求山高.(结果保留根号)
分析:(1)首先设BF=x米,过点B作BE⊥AC于E,作BF⊥CD于F,可得四边形BFCE是矩形,然后再在Rt△ABE中,求得AE与BE的长,则可用x表示出AC与CD的长,又由AC=CD,可得方程:750
+x=
x+750,解此方程即可求得答案;
(2)由(1)可知CF与DF的长,则可求得山高.
| 3 |
| 3 |
(2)由(1)可知CF与DF的长,则可求得山高.
解答: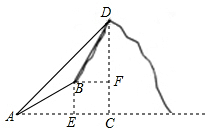 解:(1)设BF=x米,
解:(1)设BF=x米,
过点B作BE⊥AC于E,作BF⊥CD于F,
∴四边形BFCE是矩形,
∴BF=EC,CF=BE,
由题意得:∠DAC=45°,∠BAE=30°,∠DBF=60°,AB=1500米,
在Rt△ABE中,BE=
AB=750(米),AE=AB•cos∠BAE=1500×
=750
(米),
∴CF=BE=750米,
∵∠DAC=45°,DC⊥AC,
∴AC=CD,
在Rt△BDF中,BD=
=2x(米),DF=BF•tan∠DBF=
x(米),
∴750
+x=
x+750,
∴x=750,
∴BF=750米,
∴BD=1500米;
(2)∵DF=
x=750
(米),CF=750米,
∴CD=DF+CF=750
+750(米).
∴山高为(750
+750)米.
 解:(1)设BF=x米,
解:(1)设BF=x米,过点B作BE⊥AC于E,作BF⊥CD于F,
∴四边形BFCE是矩形,
∴BF=EC,CF=BE,
由题意得:∠DAC=45°,∠BAE=30°,∠DBF=60°,AB=1500米,
在Rt△ABE中,BE=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴CF=BE=750米,
∵∠DAC=45°,DC⊥AC,
∴AC=CD,
在Rt△BDF中,BD=
| BF |
| cos∠DBF |
| 3 |
∴750
| 3 |
| 3 |
∴x=750,
∴BF=750米,
∴BD=1500米;
(2)∵DF=
| 3 |
| 3 |
∴CD=DF+CF=750
| 3 |
∴山高为(750
| 3 |
点评:本题考查仰角的定义.难度适中,注意能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想与方程思想的应用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
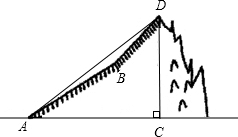 由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD.
由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD.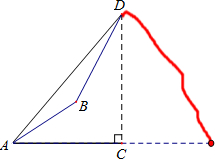 如图,由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,则山高CD为( )
如图,由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,则山高CD为( )