题目内容
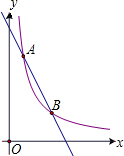 已知如图示直线y=kx+b与反比例函数y=
已知如图示直线y=kx+b与反比例函数y=| 6 |
| x |
(1)求一次函数y=kx+b的函数解析式;
(2)将一次函数y=kx+b的图象沿x轴负方向平移2个单位后,试问新图象与反比例函数y=
| 6 |
| x |
分析:(1)先把点A、B的坐标代入反比例函数解析式求出m、n的值,然后再利用待定系数法即可求出一次函数解析式;
(2)根据左加右减求出平移后的直线解析式,再与反比例函数解析式联立方程组求解,根据判别式的情况进行判断是否有交点.
(2)根据左加右减求出平移后的直线解析式,再与反比例函数解析式联立方程组求解,根据判别式的情况进行判断是否有交点.
解答:解:(1)根据题意,m=
,
=2,
解得m=6,n=3,
∴点A、B的坐标是A(1,6),B(3,2),
∴
,
解得
,
∴一次函数解析式是y=-2x+8;
(2)没有交点.
理由如下:直线沿x轴负方向平移2个单位,得y=-2(x+2)+8=-2x+4,
与反比例函数解析式联立得,
,
∴-2x+4=
,
整理得x2-2x+3=0,
△=b2-4ac=(-2)2-4×1×3=4-12=-8<0,
∴方程没有实数根,
∴新图象与反比例函数y=
的图象没有交点.
| 6 |
| 1 |
| 6 |
| n |
解得m=6,n=3,
∴点A、B的坐标是A(1,6),B(3,2),
∴
|
解得
|
∴一次函数解析式是y=-2x+8;
(2)没有交点.
理由如下:直线沿x轴负方向平移2个单位,得y=-2(x+2)+8=-2x+4,
与反比例函数解析式联立得,
|
∴-2x+4=
| 6 |
| x |
整理得x2-2x+3=0,
△=b2-4ac=(-2)2-4×1×3=4-12=-8<0,
∴方程没有实数根,
∴新图象与反比例函数y=
| 6 |
| x |
点评:本题考查了反比例函数与一次函数的交点问题,待定系数法求函数解析式,函数图象与坐标的关系,根据点A、B在是一次函数图象与反比例函数图象的交点求出m、n的值是解题的关键.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
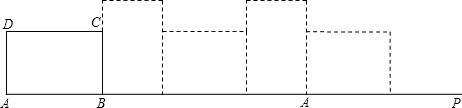


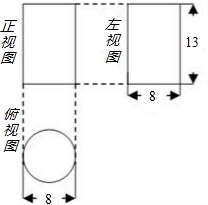 (1)已知Rt△ABC的两条直角边AC=3cm,BC=4cm,则以直线BC为轴,旋转一周所得到的几何体的侧面积是
(1)已知Rt△ABC的两条直角边AC=3cm,BC=4cm,则以直线BC为轴,旋转一周所得到的几何体的侧面积是 时它与⊙O1的位置关系是
时它与⊙O1的位置关系是