题目内容
 在△ABC中,∠ACB=90°,AB=5,tanA=
在△ABC中,∠ACB=90°,AB=5,tanA=| 4 | 3 |
(1)试判断直线PM与AC的位置关系,并证明你的结论;
(2)当Q在△ABC的外部时,已知由点Q、B、D组成的三角形与△ABC相似,求QM的长;
(3)当Q不在△ABC的边上时,设BQ=x,△BQM的面积为y,请直接写出y与x的函数关系式及函数的定义域.
分析:(1)连接CM.根据直角三角形斜边上的中线等于斜边的一半,得到BM=CM,结合PB=PC,可以根据到线段两个端点距离相等的点在线段的垂直平分线上,则PM垂直平分BC,从而PM∥AC;
(2)根据锐角三角函数的知识求得AC和BC的长,然后分三种情况考虑,再根据相似三角形的性质求解;
(3)要表示△BQM的面积,则以QM为底,高是2.根据勾股定理即可表示QM的长.
(2)根据锐角三角函数的知识求得AC和BC的长,然后分三种情况考虑,再根据相似三角形的性质求解;
(3)要表示△BQM的面积,则以QM为底,高是2.根据勾股定理即可表示QM的长.
解答: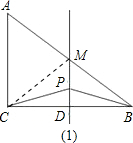 解:(1)PM∥AC.理由如下:
解:(1)PM∥AC.理由如下:
∵在△ABC中,∠ACB=90°,点M是斜边AB上的中点,
∴BM=CM,
又PB=PC,
∴PM垂直平分BC,
∴PM∥AC;
(2)①当点Q在DM的延长线上时,
∵在△ABC中,∠ACB=90°,AB=5,tanA=
,
∴AC=3,BC=4.
要使△QBD∽△BAC,
则需
=
,
即
=
,
即QD=
,
又DM=
AC=1.5,
∴QM=QD-DM=
;
②当点Q在MD的延长线上时,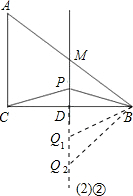
若使△QBD∽△ABC,则
=
,
即
=
,
即QD=
,
则QM=QD+DM=3;
若使△QBD∽△BAC,则
=
,
即
=
,
即QD=
,
则QM=QD+DM=
.
(3)当点Q在DM的延长线上时,
则QM=
-1.5,
则y=
-1.5(x>2.5);
当点Q在DM上时,则
y=QM=1.5-
(2<x<2.5);
当点Q在MD的延长线上时,
则y=QM=1.5+
(x>2).
 解:(1)PM∥AC.理由如下:
解:(1)PM∥AC.理由如下:∵在△ABC中,∠ACB=90°,点M是斜边AB上的中点,
∴BM=CM,
又PB=PC,
∴PM垂直平分BC,
∴PM∥AC;
(2)①当点Q在DM的延长线上时,

∵在△ABC中,∠ACB=90°,AB=5,tanA=
| 4 |
| 3 |
∴AC=3,BC=4.
要使△QBD∽△BAC,
则需
| BD |
| AC |
| QD |
| BC |
即
| 2 |
| 3 |
| QD |
| BC |
即QD=
| 8 |
| 3 |
又DM=
| 1 |
| 2 |
∴QM=QD-DM=
| 7 |
| 6 |
②当点Q在MD的延长线上时,

若使△QBD∽△ABC,则
| QD |
| AC |
| BD |
| BC |
即
| QD |
| 3 |
| 2 |
| 4 |
即QD=
| 3 |
| 2 |
则QM=QD+DM=3;
若使△QBD∽△BAC,则
| QD |
| BC |
| BD |
| AC |
即
| QD |
| 4 |
| 2 |
| 3 |
即QD=
| 8 |
| 3 |
则QM=QD+DM=
| 25 |
| 6 |
(3)当点Q在DM的延长线上时,
则QM=
| x2-4 |
则y=
| x2-4 |
当点Q在DM上时,则
y=QM=1.5-
| x2-4 |
当点Q在MD的延长线上时,
则y=QM=1.5+
| x2-4 |
点评:此题综合考查了解直角三角形的知识、相似三角形的性质、直角三角形的性质等,综合性较强.

练习册系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
 如图,在△ABC中,AC=
如图,在△ABC中,AC= 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=