Question

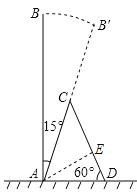
【题目】某次台风来袭时，一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断倒在地上，树的项部恰好接触到地面D(如图所示)，量得树干的倾斜角为∠BAC=15°，大树被折断部分和地面所成的角∠ADC=60°，AD=4米，求这棵大树AB原来的高度是(　　　　 )米？(结果精确到个位，参考数据：≈1.4，≈1.7，≈2.4)

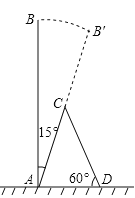
A.9B.10C.11D.12

Answer 1

【答案】B

【解析】

根据∠ADC=60°，先构建直角三角形，再解直角三角形,所以过A点作AE⊥CD于点E，则在在Rt△AED中, 利用60°的正余弦既可以求出AE、DE的长度；在Rt△ AEC中，易知∠ACE = 45°，再利用45°的正切，求出AC的长度；进而即可求取大数原来的高度.

解：过A点作AE⊥CD于点E，

∵∠BAC= 15°

∴∠DAC = 90°- 15°= 75°

∵∠ADC=60°

∴在Rt△AED中

∵cos 60°

∴

∵sin 60°

∴

∴∠EAD=90°- ∠ADE = 90°- 60°= 30°

在Rt△AEC中

∵∠CAE=∠CAD-∠DAE = 75°- 30°= 45°

∴∠ACE=90°-∠CAE = 90°- 45°= 45°

∴

∴sin45°

∴

∴

米

答:这棵大树A B原来的高度是10米.

故选B.