Question

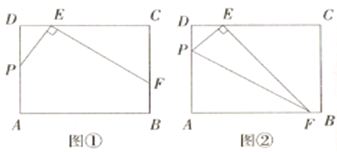
【题目】如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连接BD、DP，BD与CF相较于点H，给出下列结论：①BE=2AE；②△DFP∽△BPH；③DP2=PH·PC；④若AB=2，则S△BPD=；其中正确的是（ ）

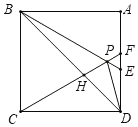
A.①②③④B.②③C.①②④D.①③④

Answer 1

【答案】A

【解析】

由等边三角形的性质和正方形的性质，得到∠ABE=∠DCF=30°，即可判断①；利用角的和差关系，根据两角对应相等，得到△DFP∽△BPH，可以判断②；由相似三角形的性质，得到，即可判断③；先得到PM和PN的长度，由面积的割补法，即可求出面积，可对④进行判断；即可得到答案.

解：∵△BPC是等边三角形，

∴BP=PC=BC，∠PBC=∠PCB=∠BPC=60°，

在正方形ABCD中，

∵AB=BC=CD，∠A=∠ADC=∠BCD=90°

∴∠ABE=∠DCF=30°，

∴BE=2AE；故①正确；

∵PC=CD，∠PCD=30°，

∴∠PDC=75°，

∴∠FDP=15°，

∵∠DBA=45°，

∴∠PBD=15°，

∴∠FDP=∠PBD，

∵∠DFP=∠BPC=60°，

∴△DFP∽△BPH；故②正确；

∵∠PDH=∠PCD=30°，∠DPH=∠DPC，

∴△DPH∽△CPD，

∴，

∴DP2=PHPC，故③正确；

如图，过P作PM⊥CD，PN⊥BC，

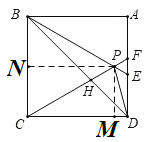
∵正方形的边长AB=2，△BPC为正三角形，

∴∠PBC=∠PCB=60°，PB=PC=BC=CD=2，

∴∠PCD=30°，

∴PN=PBsin60°=2×=，PM=PCsin30°=1，

∵S△BPD=S四边形PBCD-S△BCD=S△PBC+S△PDC-S△BCD

∴；故④正确；

∴正确的结论有：①②③④；

故选：A.