题目内容
【题目】综合与探究
问题情境
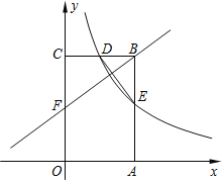
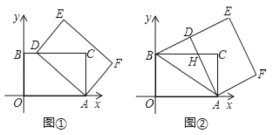
在综合实践课上，老师让同学们探究“平面直角坐标系中的旋转问题”．如图，在平面直角坐标系中，四边形
是矩形，点
，点
，点
．
操作发现
以点
为中心，顺时针旋转矩形，得到矩形
，点
，
，
的对应点分别为
，
，
．
（1）如图①，当点落在
边上时，求点的坐标；
继续探究
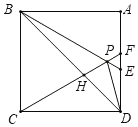
（2）如图②，当点落在线段
上时，
与交于点
．
①求证
；
②求点的坐标．
拓展探究
（3）如图①，点
是
轴上任意一点，点
是平面内任意一点，是否存在点使以、、、为顶点的四边形是菱形？若存在，请直接写出点的坐标；若不存在，请说明理由．
【答案】（1）
；（2）①见解析；②
；（3）存在，
，
，
，
【解析】
（1）根据矩形的性质得到OB＝AC＝3，OA＝BC＝5，∠C＝90°，根据旋转变换的性质得到AD＝OA＝5，根据勾股定理求出CD，得到点D的坐标；
（2）①根据旋转变换的性质得到OA＝DA，∠AOB＝∠ADE＝90°，利用HL定理证明△ADB≌△AOB；
②根据全等三角形的性质得到BD＝BO＝AC，根据△BDH≌△ACH，得到DH＝CH，根据勾股定理求出CH，得到点H的坐标；
（3）分四种情况进行讨论：①当四边形ADNM为菱形，且点N在点D左侧时；②当四边形ADNM为菱形，且点N在点D右侧时；③当四边形ADMN为菱形时，④当四边形ANDM为菱形时，根据菱形的性质即可求解．
（1）如图①中，
∵
，
，
∴
，
，
∵四边形
是矩形，
∴
，
，
，
∵矩形
是由矩形旋转得到，
∴
，
在
中，
，
∴
，
∴
（2）①如图②中，
由四边形是矩形，得到
，
点
在线段
上，
，
由（1）可知，
，又
，
，
∴
②∵
，
∴
，
又在矩形中，
，
∴
，
∴
，
∴
，设
，则
，
在
中，∵
，
∴
，
∴
，
∴
，
∴.
（3）存在，
①当四边形ADNM为菱形，且点N在点D左侧时，
∵AD=5，
∴ND=AD=AM=5，
又BD=1，
∴BN=5-1=4，
∵点M在x轴上，
∴DN∥AM，
∴N（-4,3）
②当四边形ADNM为菱形，且点N在点D右侧时，
∵AD=5，
∴ND=AD=AM=5，
又BD=1，
∴BN=5+1=6，
∵点M在x轴上，
∴DN∥AM，
∴N（6,3）
③当四边形ADMN为菱形时，
∵点M在x轴上，
∴点D与点N关于x轴对称，
∵D（1，3）,
∴N（1，-3）
④当四边形ANDM为菱形时，则MN⊥AD，
∵AM∥DC，点M在x轴上，
∴点N在BC上，DN=AN，
设CN=a，则DN=AN=4-a，
∴
,即
，解得：a=
,
∴BN=
，
故
综上所述：，，，
