Question

如图，AD是△ABC的中线，∠ADC＝45°，把△ADC沿直线AD翻折，点C落在点C ^/的位置上，如果BC＝4，那么B的长等于          ．

Answer 1

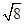
试题分析：根据翻折变换的性质可得BD=BD=D=2，∠AD＝∠ADC＝45°，即可得到△BD为等腰直角三角形，再根据勾股定理即可求得结果.
由题意得BD=BD=D=2，∠AD＝∠ADC＝45°
∴∠BD＝90°
∴
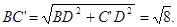
点评：解答本题的关键是熟练掌握翻折变换前后图形的对应边相等，对应角相等.