题目内容
【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.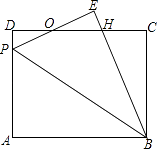
(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
【答案】
(1)解:证明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH
∴△DOP≌△EOH,
∴OP=OH,
∴PO+OE=OH+OD,
∴PE=DH;
(2)解:设DP=x,则EH=x,BH=10﹣x,
CH=CD﹣DH=CD﹣PE=10﹣(8﹣x)=2+x,
∴在Rt△BCH中,BC2+CH2=BH2
(2+x)2+82=(10﹣x)2,
∴x= ![]()
∴DP= ![]() .
.
【解析】(1)根据已知易证得△DOP≌△EOH,根据全等三角形的性质,可得到OP=OH,由OE=OD,即可得到结论。
(2)根据题意,在在Rt△BCH中,运用勾股定理,建立方程求解即可。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目