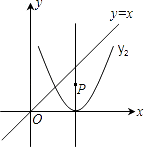题目内容
【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0) 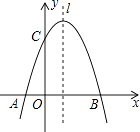
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
【答案】
(1)解:把点B的坐标为(3,0)代入抛物线y=﹣x2+mx+3得:0=﹣32+3m+3,
解得:m=2,
∴y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点坐标为:(1,4)
(2)解:连接BC交抛物线对称轴l于点P,则此时PA+PC的值最小,
设直线BC的解析式为:y=kx+b,
∵点C(0,3),点B(3,0),
∴ ![]() ,
,
解得: ![]() ,
,
∴直线BC的解析式为:y=﹣x+3,
当x=1时,y=﹣1+3=2,
∴当PA+PC的值最小时,点P的坐标为:(1,2).

【解析】(1)首先把点B的坐标为(3,0)代入抛物线y=﹣x2+mx+3,利用待定系数法即可求得m的值,继而求得抛物线的顶点坐标;(2)首先连接BC交抛物线对称轴l于点P,则此时PA+PC的值最小,然后利用待定系数法求得直线BC的解析式,继而求得答案.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

练习册系列答案
相关题目