题目内容
【题目】如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD. 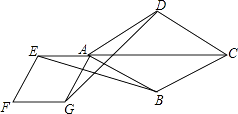
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG= ![]() ,求GD的长.
,求GD的长.
【答案】
(1)证明:∵菱形AEFG∽菱形ABCD,
∴∠EAG=∠BAD,
∴∠EAG+∠GAB=∠BAD+∠GAB,
∴∠EAB=∠GAD,
∵AE=AG,AB=AD,
∴△AEB≌△AGD,
∴EB=GD;
(2)解:连接BD交AC于点P,则BP⊥AC,
∵∠DAB=60°,
∴∠PAB=30°,
∴BP= ![]() AB=1,
AB=1,
AP= ![]() =
= ![]() ,AE=AG=
,AE=AG= ![]() ,
,
∴EP=2 ![]() ,
,
∴EB= ![]() =
= ![]() =
= ![]() ,
,
∴GD= ![]() .
.
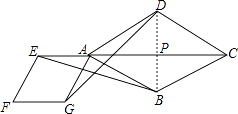
【解析】(1)利用相似多边形的对应角相等和菱形的四边相等证得三角形全等后即可证得两条线段相等;(2)连接BD交AC于点P,则BP⊥AC,根据∠DAB=60°得到BP= ![]() AB=1,然后求得EP=2
AB=1,然后求得EP=2 ![]() ,最后利用勾股定理求得EB的长即可求得线段GD的长即可.
,最后利用勾股定理求得EB的长即可求得线段GD的长即可.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

【题目】我市启动了第二届“美丽港城,美在阅读”全民阅读活动,为了解市民每天的阅读时间情况,随机抽取了部分市民进行调查,根据调查结果绘制如下尚不完整的频数分布表:
阅读时间 | 0≤x<30 | 30≤x<60 | 60≤x<90 | x≥90 | 合计 |
频数 | 450 | 400 | 50 | ||
频率 | 0.4 | 0.1 | 1 |
(1)补全表格;
(2)将每天阅读时间不低于60min的市民称为“阅读爱好者”,若我市约有500万人,请估计我市能称为“阅读爱好者”的市民约有多少万人?