题目内容
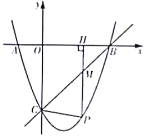
【题目】如图,在平面直角坐标系中,点A(m,n)(m>0)在双曲线y=![]() 上.
上.
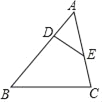
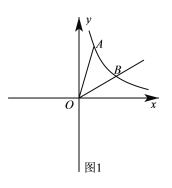
(1)如图1,m=1,∠AOB=45°,点B正好在y=![]() (x>0)上,求B点坐标;
(x>0)上,求B点坐标;
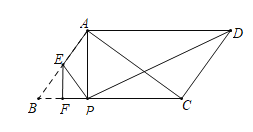
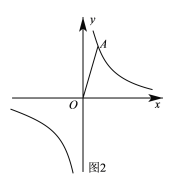
(2)如图2,线段OA绕O点旋转至OC,且C点正好落在y=![]() 上,C(a,b),试求m与a的数量关系.
上,C(a,b),试求m与a的数量关系.
【答案】(1)B(![]() ,
,![]() );(2)
);(2)![]() 或
或![]() ,
,![]()
【解析】
(1)作出辅助线如图,证得Rt△FAO![]() Rt△DAG,求得点G的坐标为(5,3),继而求得直线OG的解析式,从而求得点B的坐标;
Rt△DAG,求得点G的坐标为(5,3),继而求得直线OG的解析式,从而求得点B的坐标;
(2)由题意得A(m,![]() ),C(a,
),C(a,![]() ),OA2=OC2,计算整理得(m2-a2)(1-
),OA2=OC2,计算整理得(m2-a2)(1-![]() )=0,即可求解.
)=0,即可求解.
(1)∵点A(m,n)在双曲线y=![]() 上,且m=1,
上,且m=1,
∴![]() ,
,
∴点A的坐标为(1,4),
作AG⊥OA交直线OB于点G,作GE⊥y轴于E,作AF⊥y轴于F,作AD⊥![]() 轴交GE于点D,如图所示:
轴交GE于点D,如图所示:
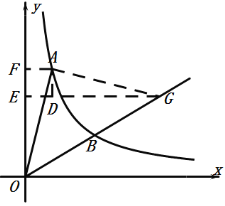
∵点A的坐标为(1,4),
∴FA=1,FO=4,
∵AG⊥OA,∠AOB=45°,
∴△AOG为等腰直角三角形,
∴AO=AG,
∵∠FAO+∠OAD=∠DAG+∠OAD=90°,
∴∠FAO=∠DAG,
∴Rt△FAO![]() Rt△DAG,
Rt△DAG,
∴FO= DG=4,FA=DA=1,
∵GE⊥y轴, AF⊥y轴,AD⊥![]() 轴,FA=DA=1,
轴,FA=DA=1,
∴四边形ADEF为正方形,
∴FA=DA= DE=EF=1,
∴GE=DE+DG=5,EO=FO-EF=3,
∴点G的坐标为(5,3),
设直线OG的解析式为![]() ,
,
把点G的坐标为(5,3)代入得:![]() ,
,
∴直线OG的解析式为![]() ,
,
解方程组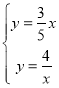 ,
,
得: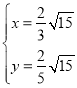 (负值已舍),
(负值已舍),
∴点B的坐标为(![]() ,
,![]() );
);
(2)根据题意:A(m,![]() ),C(a,
),C(a,![]() ),
),
∵OA2=OC2,
∴m2+![]() =
=![]() 2+
2+![]() ,
,
整理得:(m2-a2)(1-![]() )=0,(
)=0,(![]() )(
)(![]() )(
)(![]() )(
)(![]() )=0,
)=0,
∵![]() ,
,
∴![]() 或
或![]() ,
,![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目