题目内容
如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2,垂足为D,过点O,B的直线l4交l2于点E,当直线l1,l2,l3能围成三角形时,设该三角形面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形面积为S2.
(1)若点B在线段AC上,且S1=S2,则B点坐标为______;
(2)若点B在直线l1上,且S2=
S1,则∠BOA的度数为______.

(1)若点B在线段AC上,且S1=S2,则B点坐标为______;
(2)若点B在直线l1上,且S2=
| 3 |

(1)设B的坐标是(2,m),
∵直线l2:y=x+1交l1于点C,
∴∠ACE=45°,
∴△BCD是等腰直角三角形.
BC=|3-m|,
则BD=CD=
BC=
|3-m|,
S1=
×(
|3-m|)2=
(3-m)2.
设直线l4的解析式是y=kx,过点B,
则2k=m,解得:k=
,
则直线l4的解析式是y=
x.
根据题意得:
,解得:
,
则E的坐标是(
,
).
S△BCE=
BC•|
-2|=
|3-m|•|
|=
.
∴S2=S△BCE-S1=
-
(3-m)2.
当S1=S2时,
-
(3-m)2=
(3-m)2.
解得:m1=4或m2=0,
易得点C坐标为(2,3),即AC=3,
∵点B在线段AC上,
∴m1=4不合题意舍去,
则B的坐标是(2,0);
(2)分三种情况:
①当点B在线段AC上时
当S2=
S1时,
-
(3-m)2=
(3-m)2.
解得:m=4-2
或2
(不在线段AC上,舍去),或m=3(l2和l4重合,舍去).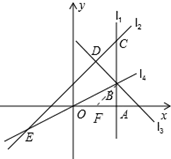
则AB=4-2
.
在OA上取点F,使OF=BF,连接BF,设OF=BF=x.
则AF=2-x,根据勾股定理,x2=(2-x)2+(4-2
)2,
解得:x=8-4
,
∴sin∠BFA=
=
,
∴∠BFA=30°,
∴∠BOA=15°;
②当点B在AC延长线上时,
此时,S2=S△BCE+S1=
+
(3-m)2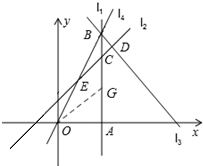
当S2=
S1时,得:
+
(3-m)2=
?
(3-m)2,
解得符合题意有:AB=4+2
.
在AB上取点G,使BG=OG,连接OG,设BG=OG=x,
则AG=4+2
-x.根据勾股定理,得x2=(4+2
-x)2+22,
解得:x=4,
∴sin∠OGA=
=
,
∴∠OGA=30°,
∴∠OBA=15°,
∴∠BOA=75°;

③当点B在CA延长线上时
此时,S2=S1-S△BCE=
(3-m)2-
,
当S2=
S1时,得:
(3-m)2-
=
?
(3-m)2,
解得:m=3(l2和l4重合,舍去),
∴此时满足条件的点B不存在,
综上所述,∠BOA的度数为15°或75°.
∵直线l2:y=x+1交l1于点C,
∴∠ACE=45°,
∴△BCD是等腰直角三角形.
BC=|3-m|,
则BD=CD=
| ||
| 2 |
| ||
| 2 |
S1=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
设直线l4的解析式是y=kx,过点B,
则2k=m,解得:k=
| m |
| 2 |
则直线l4的解析式是y=
| m |
| 2 |
根据题意得:
|
|
则E的坐标是(
| 2 |
| m-2 |
| m |
| m-2 |
S△BCE=
| 1 |
| 2 |
| 2 |
| m-2 |
| 1 |
| 2 |
| 6-2m |
| m-2 |
| (3-m)2 |
| |m-2| |
∴S2=S△BCE-S1=
| (3-m)2 |
| |m-2| |
| 1 |
| 4 |
当S1=S2时,
| (3-m)2 |
| |m-2| |
| 1 |
| 4 |
| 1 |
| 4 |
解得:m1=4或m2=0,
易得点C坐标为(2,3),即AC=3,
∵点B在线段AC上,
∴m1=4不合题意舍去,
则B的坐标是(2,0);
(2)分三种情况:
①当点B在线段AC上时
当S2=
| 3 |
| (3-m)2 |
| |m-2| |
| 1 |
| 4 |
| ||
| 4 |
解得:m=4-2
| 3 |
| 3 |

则AB=4-2
| 3 |
在OA上取点F,使OF=BF,连接BF,设OF=BF=x.
则AF=2-x,根据勾股定理,x2=(2-x)2+(4-2
| 3 |
解得:x=8-4
| 3 |
∴sin∠BFA=
4-2
| ||
8-4
|
| 1 |
| 2 |
∴∠BFA=30°,
∴∠BOA=15°;
②当点B在AC延长线上时,
此时,S2=S△BCE+S1=
| (3-m)2 |
| |m-2| |
| 1 |
| 4 |

当S2=
| 3 |
| (3-m)2 |
| |m-2| |
| 1 |
| 4 |
| 3 |
| 1 |
| 4 |
解得符合题意有:AB=4+2
| 3 |
在AB上取点G,使BG=OG,连接OG,设BG=OG=x,
则AG=4+2
| 3 |
| 3 |
解得:x=4,
∴sin∠OGA=
| 2 |
| 4 |
| 1 |
| 2 |
∴∠OGA=30°,
∴∠OBA=15°,
∴∠BOA=75°;

③当点B在CA延长线上时
此时,S2=S1-S△BCE=
| 1 |
| 4 |
| (3-m)2 |
| |m-2| |
当S2=
| 3 |
| 1 |
| 4 |
| (3-m)2 |
| |m-2| |
| 3 |
| 1 |
| 4 |
解得:m=3(l2和l4重合,舍去),
∴此时满足条件的点B不存在,
综上所述,∠BOA的度数为15°或75°.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目

 的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.


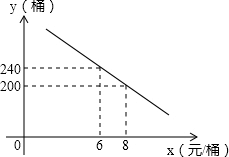 费用是a元.
费用是a元.