题目内容
等腰△ABC中，AB=AC，O是腰AB上一点（不同于A、B），以OB为半径，作圆交边BC于D，E是边AC上一点，连接DE，①若AB是⊙O的直径，且DE是⊙O的切线，则DE⊥AC；②若AB是⊙O的直径，且DE⊥AC，则DE是⊙O的切线；③若DE是⊙O的切线，且DE⊥AC，则AB是⊙O的直径．
上述命题中，正确的命题是（ ）
上述命题中，正确的命题是（ ）
| A、①②③ | B、①② | C、①③ | D、②③ |
分析：利用每一个命题的前提作为已知条件，看看能不能推出结论即可．
解答：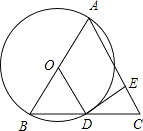
解：根据题意作图
①：若AB为直径，DE为切线?OD=
AC，且OD为△ABC的中位线，即OD∥AC，
∴DE⊥AC，①正确，
②：若AB为直径?OD∥AC，
又∵DE⊥AC，
∴DE⊥OD，
∴DE为是⊙O的切线，②正确，
③：由前提只能推出OD∥AC，不能推出AB是⊙O的直径，故命题错误．
故选B．
解：根据题意作图①：若AB为直径，DE为切线?OD=
| 1 |
| 2 |
∴DE⊥AC，①正确，
②：若AB为直径?OD∥AC，
又∵DE⊥AC，
∴DE⊥OD，
∴DE为是⊙O的切线，②正确，
③：由前提只能推出OD∥AC，不能推出AB是⊙O的直径，故命题错误．
故选B．
点评：本题考查了圆与三角形的知识，注意利用作图直观推理判断．
练习册系列答案
阅读快车系列答案
相关题目
24、等腰△ABC中，AB=AC，D为BC上的一动点，DE∥AC，DF∥AB，分别交AB于E，AC于F，则DE+DF是否随D点变化而变化？请说明理由．
如图，在等腰△ABC中，AB=AC，以AB为直径作⊙O交BC于D，交AC于E，过D点作DF⊥AC于F，有下列结论：
如图，在等腰△ABC中，AB=AC，∠A=50°，边AB的垂直平分线交边AC于点E，则∠EBC=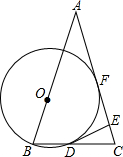
如图，在等腰△ABC中，AB=AC，O为AB上一点，以O为圆心，OB长为半径的圆交BC于D，DE⊥AC交AC于点E．