题目内容
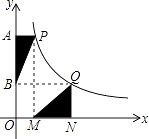
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2 ![]() ?若存在求出点Q的坐标;若不存在请说明理由.
?若存在求出点Q的坐标;若不存在请说明理由.
【答案】
(1)
解:∵抛物线的顶点C的坐标为(1,4),
∴可设抛物线解析式为y=a(x﹣1)2+4,
∵点B(3,0)在该抛物线的图象上,
∴0=a(3﹣1)2+4,解得a=﹣1,
∴抛物线解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3,
∵点D在y轴上,令x=0可得y=3,
∴D点坐标为(0,3),
∴可设直线BD解析式为y=kx+3,
把B点坐标代入可得3k+3=0,解得k=﹣1,
∴直线BD解析式为y=﹣x+3
(2)
解:设P点横坐标为m(m>0),则P(m,﹣m+3),M(m,﹣m2+2m+3),
∴PM=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,PM有最大值
时,PM有最大值 ![]()
(3)
解:如图,过Q作QG∥y轴交BD于点G,交x轴于点E,作QH⊥BD于H,

设Q(x,﹣x2+2x+3),则G(x,﹣x+3),
∴QG=|﹣x2+2x+3﹣(﹣x+3)|=|﹣x2+3x|,
∵△BOD是等腰直角三角形,
∴∠DBO=45°,
∴∠HGQ=∠BGE=45°,
当△BDQ中BD边上的高为2 ![]() 时,即QH=HG=2
时,即QH=HG=2 ![]() ,
,
∴QG= ![]() ×2
×2 ![]() =4,
=4,
∴|﹣x2+3x|=4,
当﹣x2+3x=4时,△=9﹣16<0,方程无实数根,
当﹣x2+3x=﹣4时,解得x=﹣1或x=4,
∴Q(﹣1,0)或(4,﹣5),
综上可知存在满足条件的点Q,其坐标为(﹣1,0)或(4,﹣5)
【解析】(1)可设抛物线解析式为顶点式,由B点坐标可求得抛物线的解析式,则可求得D点坐标,利用待定系数法可求得直线BD解析式;(2)设出P点坐标,从而可表示出PM的长度,利用二次函数的性质可求得其最大值;(3)过Q作QG∥y轴,交BD于点G,过Q和QH⊥BD于H,可设出Q点坐标,表示出QG的长度,由条件可证得△DHG为等腰直角三角形,则可得到关于Q点坐标的方程,可求得Q点坐标.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案