题目内容
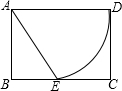 如图,已知矩形纸片ABCD,AD=2,AB=
如图,已知矩形纸片ABCD,AD=2,AB=| 3 |
分析:易得∠BAE的余弦值,也就求得了∠BAE的度数,进而可求得∠DAE的度数,利用弧长公式可求得圆锥的侧面展开图的弧长,除以2π即为圆锥的底面半径.
解答:解:cos∠BAE=
=
,
∴∠BAE=30°,
∴∠DAE=60°,
∴圆锥的侧面展开图的弧长为:
=
π,
∴圆锥的底面半径为
π÷2π=
.
| AB |
| AE |
| ||
| 2 |
∴∠BAE=30°,
∴∠DAE=60°,
∴圆锥的侧面展开图的弧长为:
| 60π×2 |
| 180 |
| 2 |
| 3 |
∴圆锥的底面半径为
| 2 |
| 3 |
| 1 |
| 3 |
点评:用到的知识点为:圆锥的侧面展开图的弧长等于圆锥的底面周长;圆锥的底面半径等于底面周长除以2π.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


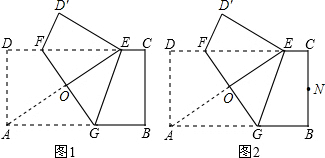 A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.
A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.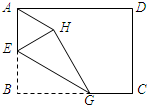 (2012•安庆二模)如图,已知矩形纸片ABCD,E是AB边的中点,点G为BC边上的一点,现沿EG将纸片折叠,使点B落在纸片上的点H处,连接AH.若AB=EG,则与∠BEG相等的角的个数为( )
(2012•安庆二模)如图,已知矩形纸片ABCD,E是AB边的中点,点G为BC边上的一点,现沿EG将纸片折叠,使点B落在纸片上的点H处,连接AH.若AB=EG,则与∠BEG相等的角的个数为( )