��Ŀ����
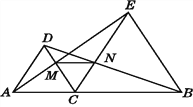
����Ŀ����ͼ��ʾ��A��B���������ϱ��������еĵ��߸ˣ�A��B֮����һ��С�ӣ�С����������������߸�֮��ľ��룬����С�մ�A�㿪ʼ��������������20������һ�ô���C������������ǰ����20������D����Ȼ������ת90��ֱ�У������������߸�B������C�����Լ�����������λ��Eǡ��ͬһ��ֱ����ʱ������Dλ���ߵ�E��ǡ������100���������������ݣ�С�ղ����A��B�������߸�֮��ľ��룮
(1)������������IJ���������ԭͼ�ϻ���ʾ��ͼ��
(2)���С��һ����Լ60���ף�������A��B�������߸�֮��ľ��벢�������ɣ�
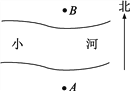
���𰸡�(1)ͼ�ԡ�(2)AB��60m
����������������1��������⣬�������⻭��ʾ��ͼ����2���������ֱ����AC��DC��DE�ij����ã�AC=DC����BAC=��EDC����DCE=��ACB������ȫ�������ε��ж������ɵá�ABC�ա�DEC�������õ�AB=DE���ݴˣ��ɵó����.
�����������1���������⻭��ͼ�Σ���ͼ��ʾ.
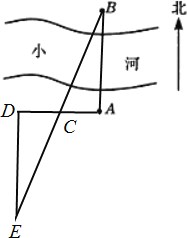
��2��A��B�������߸�֮��ľ����ԼΪ36m.��������.
�ߡ�BAC=��EDC=90�㣬60cm=0.6m��
��AC=20��0.6=12m��
DC=20��0.6=12m��
DE=100��0.6=60m.
�ߵ�E��C��B��һ��ֱ���ϣ�
���DCE=��ACB.
�ߡ�BAC=��EDC=90�㣬AC=DC����DCE=��ACB��
���ABC�ա�DEC.
��AB=DE.
��AB=DE��DE=60m��
��AB=60m.
��A��B�������߸�֮��ľ����ԼΪ60m.