题目内容
【题目】(1)当a=2,b=![]() 时,分别求代数式(ab)2和a2-2ab+b2的值.
时,分别求代数式(ab)2和a2-2ab+b2的值.
(2)当a=1,b=5时,分别求代数式(ab)2和a2-2ab+b2的值;
(3)观察(1)(2)中代数式的值,a2-2ab+b2与(ab)2有何关系?
(4)利用你发现的规律,求135.72-2×135.7×35.7+35.72的值.
【答案】(1)![]() ;(2)36;(3)a2-2ab+b2=(ab)2;(4)10000.
;(2)36;(3)a2-2ab+b2=(ab)2;(4)10000.
【解析】试题分析:(1)(2)直接代入a、b的值求代数式的值;(3)由(1)(2)找出规律,得出a2-2ab+b2与(a-b)2的关系;(4)由(3)得出的规律,直接求出所要求的式子即可.
解:(1)当a=2,b=![]() 时,(ab)2=(2
时,(ab)2=(2![]() )2=(
)2=(![]() )2=
)2=![]() ,
,
a2-2ab+b2=222×2×![]() +(
+(![]() )2=
)2=![]() ;
;
(2)当a=1,b=5时,(ab)2=(15)2=36,
a2-2ab+b2=(1)22×(1)×5+52=36;
(3)观察(1)(2)可得a2-2ab+b2=(ab)2;
(4)由(3)的结论可得135.72-2×135.7×35.7+35.72=(135.735.7)2=1002=10000.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
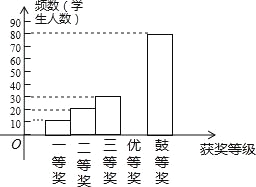
波波熊暑假作业江西人民出版社系列答案【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= ,b= ,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
【题目】在某次试验数据整理过程中,某个事件发生的频率情况如表所示.
试验次数 | 10 | 50 | 100 | 200 | 500 | 1000 | 2000 |
事件发生的 | 0.245 | 0.248 | 0.251 | 0.253 | 0.249 | 0.252 | 0.251 |
估计这个事件发生的概率是(精确到0.01).
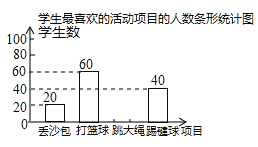
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息,解答下列问题:
(1)m= ,n= ,p= ;
(2)请根据以上信息直接补全条形统计图;
(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.