题目内容
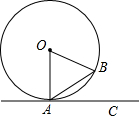
如图，在边长为2的等边三角形ABC中，以B为圆心，AB为半径作
，在扇形BAC内作⊙O与AB、BC、
都相切，则⊙O的周长等于（ ）
 |
| AC |
|
| AC |
A．
| B．
| C．
| D．π |
连接OB并延长与
交于点E，设AB与圆的切点为D，连接OD，
∵△ABC为等边三角形，以B为圆心，AB为半径作
，
∴∠ABC=60°，BA=BC=BE=2，
由对称性得到：∠ABE=30°，
∵AB为圆O的切线，
∴OD⊥AB，
在Rt△BOD中，∠ABE=30°，设OD=OE=x，
可得OB=2x，
∴OB+OE=BE，即2x+x=2，
解得：x=
，即圆O的半径为
，
则圆O的周长为
π．
故选C．
|
| AC |
∵△ABC为等边三角形，以B为圆心，AB为半径作
|
| AC |
∴∠ABC=60°，BA=BC=BE=2，
由对称性得到：∠ABE=30°，
∵AB为圆O的切线，
∴OD⊥AB，
在Rt△BOD中，∠ABE=30°，设OD=OE=x，
可得OB=2x，
∴OB+OE=BE，即2x+x=2，
解得：x=
| 2 |
| 3 |
| 2 |
| 3 |
则圆O的周长为
| 4 |
| 3 |
故选C．
练习册系列答案
相关题目
段PC于点E，且PD=PE．
