题目内容
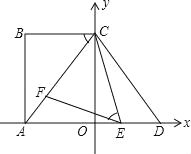
【题目】如图:在平面直角坐标系中,点A、C分别在x轴负半轴、y轴正半轴上,且四边形ABCD为矩形,AB=4,点D与点A关于原点O成中心对称,tan∠ACB=![]() ,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
(1)求AC的长和点D的坐标;
(2)说明△AEF与△DCE相似;
(3)点M在第二象限,且在直线BC的下方,点N在平面内,是否存在这样点M,使得以点B、C、M、N为顶点的四边形是矩形,且矩形的长:宽=4:3?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)5;D(3,0);(2)证明见解析;(3)存在,M的坐标是(-3,![]() ).
).
【解析】
试题分析:(1)由tan∠ACB的值,求出cos∠ACB的值,再由矩形ABCO,以及AB的长,求出BC与AC的长,利用对称性确定出D坐标即可;
(2)由对称性得到∠CDE=∠CAO,利用等式的性质得到一对角相等,利用两角相等的三角形相似即可得证;
(3)根据题意得到点M在线段AB上,点N在y轴上,由于矩形的长:宽=4:3,得到![]() ,或
,或![]() ,求得BM=
,求得BM=![]() 或BM=4(不合题意,舍去),于是得到结论.
或BM=4(不合题意,舍去),于是得到结论.
试题解析:(1)由题意tan∠ACB=![]() ,
,
∴cos∠ACB=![]() .
.
∵四边形ABCO为矩形,AB=4,
∴BC=![]() =3,AC=
=3,AC=![]() =5,
=5,
∴A点坐标为(-3,0),
∵点D与点A关于y轴对称,
∴D(3,0);
(2)点D与点A关于y轴对称,∴∠CDE=∠CAO,
∵∠CEF=∠ACB,∠ACB=∠CAO,
∴∠CDE=∠CEF,
又∵∠AEC=∠AEF+∠CEF=∠CDE+∠DCE(三角形外角性质)
∴∠AEF=∠DCE.
则在△AEF与△DCE中,∠CDE=∠CAO,∠AEF=∠DCE,
∴△AEF∽△DCE;
(3)存在,如图,
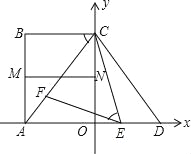
∵点M在第二象限,且在直线BC的下方,点N在平面内,
∵B、C、M、N为顶点的四边形是矩形,
∴点M在线段AB上,点N在y轴上,
∵矩形的长:宽=4:3,
∴![]() ,或
,或![]() ,
,
∵BC=3,
∴BM=![]() 或BM=4(不合题意,舍去),
或BM=4(不合题意,舍去),
∴M的坐标是(-3,![]() ).
).