Question

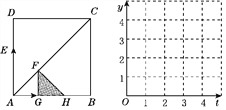
【题目】如图，正方形ABCD的边长为4，动点E从点A出发，以每秒2个单位的速度沿A→D→A运动，动点G从点A出发，以每秒1个单位的速度沿A→B运动，当有一个点到达终点时，另一点随之也停止运动．过点G作FG⊥AB交AC于点F.设运动时间为t(单位：秒)．以FG为一直角边向右作等腰直角三角形FGH，△FGH与正方形ABCD重叠部分的面积为S.

(1)当t＝1.5时，S＝________；当t＝3时，S＝________.

(2)设DE＝y1，AG＝y2，在如图所示的网格坐标系中，画出y1与y2关于t的函数图象．并求当t为何值时，四边形DEGF是平行四边形？

Answer 1

【答案】（1）； ；（2）当t＝或t＝4时，四边形DEGF是平行四边形．

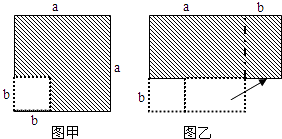
【解析】试题分析：（1）当t＝1.5时，如图①，重叠部分的面积是△FGH的面积，求出即可；当t＝3时，如图②，重叠部分的面积是四边形FGBK的面积，也就是△FGH的面积减去△KBH的面积，求出即可；

（2）进行分类讨论，列出方程即可求出t的值.

试题解析：当t＝1.5时，如图①，重叠部分的面积是△FGH的面积，所以S＝；

当t＝3时，如图②，重叠部分的面积是四边形FGBK的面积，也就是△FGH的面积减去△KBH的面积，所以S＝×3×3－×2×2＝.

(2)由题意可以求得

y1＝ ；y2＝t(0≤t≤4)．<

所以y1与y2关于t的函数图象如图③所示．

因为运动过程中，DE∥FG，所以当DE＝FG时，四边形DEGF是平行四边形．

∵FG＝AG，

∴DE＝AG，

∴y1＝y2.由图象可知，有两个t值满足条件：

①当0≤t≤2时，由4－2t＝t，解得t＝；

②当2<t≤4时，由2t－4＝t，解得t＝4.　

所以当t＝或t＝4时，四边形DEGF是平行四边形．