题目内容
抛物线y=x2-2x+1与坐标轴交点个数为（ ）
| A、无交点 | B、1个 | C、2个 | D、3个 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
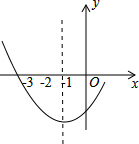如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=-1，且过点（-3，0）下列说法：①abc＜0；②2a-b=0；③4a+2b+c＜0；④若（-5，y1），（2，y2）是抛物线上的两点，则y1＞y2．
其中说法正确的是（ ）
| A、①② | B、②③ | C、②③④ | D、①②④ |
将抛物线y=3（x-2）2向左平移3个单位得到的抛物线的解析式是（ ）
| A、y=3（x-5）2 | B、y=3（x-2）2+3 | C、y=3（x+1）2 | D、y=3（x-2）2-3 |
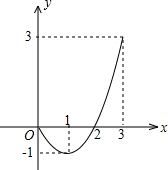已知二次函数的图象（0≤x≤3）如图．关于该函数在所给自变量取值范围内，下列说法正确的是（ ）| A、有最小值0，有最大值3 | B、有最小值-1，有最大值0 | C、有最小值-1，有最大值3 | D、有最小值-1，无最大值 |
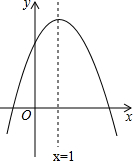如图，抛物线y=ax2+bx+c与x轴交于点A（-1，0），顶点坐标为C（1，k），与y轴的交点在（0，2）、（0，3）之间（不包含端点），则k的取值范围是（ ）| A、2＜k＜3 | ||
B、
| ||
C、
| ||
| D、3＜k＜4 |
若二次函数y=ax2+bx+c（a≠0）的图象于x轴的交点坐标分别为（x1，0），（x2，0），且x1＜x2，图象上有一点M（x0，y0）在x轴下方，对于以下说法：
①b2-4ac＞0；②x=x0是方程ax2+bx+c=y0的解；③x1＜x0＜x2；④a（x0-x1）（x0-x2）＜0．
其中正确的是（ ）
①b2-4ac＞0；②x=x0是方程ax2+bx+c=y0的解；③x1＜x0＜x2；④a（x0-x1）（x0-x2）＜0．
其中正确的是（ ）
| A、①③④ | B、①②④ | C、①②③ | D、②③ |
在平面直角坐标系xOy中，直线y=kx（k为常数）与抛物线y=
x2-2交于A，B两点，且A点在y轴左侧，P点的坐标为（0，-4），连接PA，PB．有以下说法：
①PO2=PA•PB；
②直线PA、PB关于y轴对称；
③当k=
时，BP2=BO•BA；
④△PAB面积的最小值为4
，
其中正确的是（写出所有正确说法的序号）（ ）
| 1 |
| 3 |
①PO2=PA•PB；
②直线PA、PB关于y轴对称；
③当k=
| ||
| 3 |
④△PAB面积的最小值为4
| 6 |
其中正确的是（写出所有正确说法的序号）（ ）
| A、①，③，④ | B、②，③ |
| C、②，④ | D、②，③，④ |
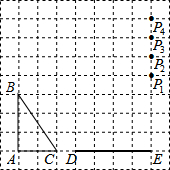如图，在方格纸中，△ABC和△EPD的顶点均在格点上，要使△ABC∽△EPD，则点P所在的格点为（ ）| A、P1 | B、P2 | C、P3 | D、P4 |
如图，四边形ABCD是矩形，点E和点F是矩形ABCD外两点，AE⊥CF于点H，AD=3，DC=4，DE=| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|