题目内容

在平面直角坐标系xOy中，直线y=kx（k为常数）与抛物线y=
1
3
x2-2交于A，B两点，且A点在y轴左侧，P点的坐标为（0，-4），连接PA，PB．有以下说法：
①PO2=PA•PB；
②直线PA、PB关于y轴对称；
③当k=
3
3
时，BP2=BO•BA；
④△PAB面积的最小值为4
6
，
其中正确的是（写出所有正确说法的序号）（　　）
A、①，③，④B、②，③
C、②，④D、②，③，④
练习册系列答案
相关题目
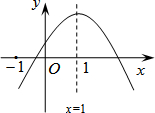已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列结论：
①ac＞0； 
②a-b+c＜0； 
③当x＜0时，y＜0；
④方程ax2+bx+c=0（a≠0）有两个大于-1的实数根．
其中错误的结论有（　　）
A、①③B、②③C、①④D、②④
将抛物线y=x2-2平移到抛物线y=x2+2x-2的位置，以下描述正确的是（　　）
A、向左平移1单位，向上平移1个单位B、向右平移1单位，向上平移1个单位C、向左平移1单位，向下平移1个单位D、向右平移1单位，向下平移1个单位
抛物线y=x2-2x+1与坐标轴交点个数为（　　）
A、无交点B、1个C、2个D、3个
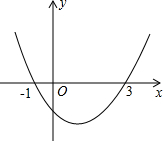二次函数y=ax2+bx+c（a≠0）的图象如图所示，则函数值y＞0时，x的取值范围是（　　）
A、x＜-1B、x＞3C、-1＜x＜3D、x＜-1或x＞3
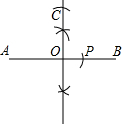如图，画线段AB的垂直平分线交AB于点O，在这条垂直平分线上截取OC=OA，以A为圆心，AC为半径画弧于AB与点P，则线段AP与AB的比是（　　）
A、
3
：2
B、1：
3
C、
2
：
3
D、
2
：2
如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，且DE∥BC，EF∥AB．若AD=2BD，则
CF
BF
的值为（　　）
A、
1
2
B、
1
3
C、
1
4
D、
2
3
如图，小明在打网球时，使球恰好能打过网，而且落在离网4米的位置上，则球拍击球的高度h为（　　）
A、1.6米B、1.5米C、2.4米D、1.2米
如图，已知：在边长为12的正方形ABCD中，有一个小正方形EFGH，其中E，F，G分别在AB，BC，FD上，若BF=3，则BE长为（　　）
A、
12
B、
15
4
C、5
D、
9
4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网