题目内容
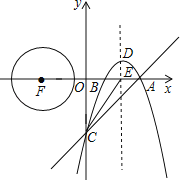
【题目】如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 经过
经过![]() 三点,抛物线的顶点为点
三点,抛物线的顶点为点![]() ,对称轴与
,对称轴与![]() 轴的交点为点
轴的交点为点![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,连接
,连接![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作圆,点
的长为半径作圆,点![]() 为直线
为直线![]() 上的一个动点.
上的一个动点.
(1)求抛物线的解析式;
(2)求![]() 周长的最小值;
周长的最小值;
(3)若动点![]() 与点
与点![]() 不重合,点
不重合,点![]() 为⊙
为⊙![]() 上的任意一点,当
上的任意一点,当![]() 的最大值等于
的最大值等于![]() 时,过
时,过![]() 两点的直线与抛物线交于
两点的直线与抛物线交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),求四边形
的左侧),求四边形![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() (3)
(3)![]()
【解析】
(1)直线y=x-3,令x=0,则y=-3,令y=0,则x=3,故点A、C的坐标为(3,0)、(0,-3),即可求解;
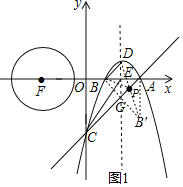
(2)过点B作直线y=x-3的对称点B′,连接BD交直线y=x-3于点P,直线B′B交函数对称轴与点G,则此时△BDP周长=BD+PB+PD=BD+B′B为最小值,即可求解;
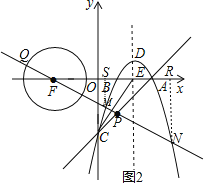
(3)如图2所示,连接PF并延长交圆与点Q,此时PQ为最大值,即可求解.
解:(1)直线![]() ,令
,令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
故点![]() 的坐标为
的坐标为![]() 、
、![]() ,
,
则抛物线的表达式为:![]() ,
,
则![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:![]() …①;
…①;
(2)过点![]() 作直线
作直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 交直线
交直线![]() 于点
于点![]() ,
,
直线![]() 交函数对称轴与点
交函数对称轴与点![]() ,连接
,连接![]() ,
,
则此时![]() 周长
周长![]() 为最小值,
为最小值,
![]() ,则点
,则点![]() ,即:
,即:![]() ,
,
即点![]() 是
是![]() 的中点,过点
的中点,过点![]() ,
,
![]() 周长最小值
周长最小值![]() ;
;
(3)如图2所示,连接![]() 并延长交圆与点
并延长交圆与点![]() ,此时
,此时![]() 为最大值,
为最大值,
点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,![]() ,
,
则![]() ,
,
设点![]() ,点
,点![]() ,
,
![]() ,
,
解得:![]() ,故点
,故点![]() ,
,
将点![]() 坐标代入一次函数表达式并解得:
坐标代入一次函数表达式并解得:
直线![]() 的表达式为:
的表达式为:![]() …②,
…②,
联立①②并解得:![]() ,
,
故点![]() 的坐标分别为:
的坐标分别为:
过点![]() 分别作
分别作![]() 轴的垂线交于点
轴的垂线交于点![]() ,
,
则![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目