题目内容
如图，∠B=90°，AB=4cm，BC=3cm，CD=12cm，AD=13cm，则图中由四条线段围成的图形的面积是________cm2．
24
分析：连接AC，因为∠B=90°，AB=4cm，BC=3cm，CD=12cm，AD=13cm，利用勾股定理可求出AC的长，然后利用勾股定理的逆定理即可判断出∠ACD=90°，那么所求的图形面积=△ACD的面积-△ACB的面积．
解答：
解：连接AC，因为∠B=90°，AB=4cm，BC=3cm，CD=12cm，AD=13cm
所以AC=5cm，且AC2+CD2=AD2，所以∠ACD=90°，
所以所求的图形面积=△ACD的面积-△ACB的面积=
=24cm2．
点评：本题需仔细分析图形，利用勾股定理及其逆定理来解决问题．
分析：连接AC，因为∠B=90°，AB=4cm，BC=3cm，CD=12cm，AD=13cm，利用勾股定理可求出AC的长，然后利用勾股定理的逆定理即可判断出∠ACD=90°，那么所求的图形面积=△ACD的面积-△ACB的面积．
解答：
解：连接AC，因为∠B=90°，AB=4cm，BC=3cm，CD=12cm，AD=13cm所以AC=5cm，且AC2+CD2=AD2，所以∠ACD=90°，
所以所求的图形面积=△ACD的面积-△ACB的面积=
=24cm2．点评：本题需仔细分析图形，利用勾股定理及其逆定理来解决问题．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
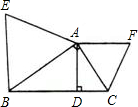如图，∠BAC=90°，AD⊥BC，△ABE，△ACF都是等边三角形，则S△ABE：S△ACF等于（ ）| A、AB：AC | B、AD2：DC2 | C、BD2：DC2 | D、AC2：AB2 |
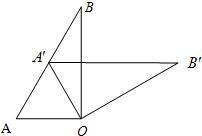14、如图，∠AOB=90°，∠B=30°，△AOB′可以看作是由△AOB绕点O顺时针旋转α角度得到的，若点A′在AB上，则旋转角α的大小可以是
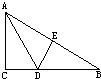16、如图，∠C=90°，AD平分∠CAB，DE⊥AB于E，若DB=2DE=6cm，则BC=
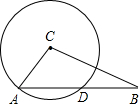已知：如图，∠C=90°，⊙C与AB相交于点D，AC=5，CB=12，求AD．
如图，∠AOB=90°，0C⊥OD，且∠BOC=