题目内容
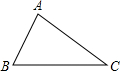 如图所示,已知△ABC中,AB<AC<BC.求作:一圆的圆心O,使得O在BC上,且圆O与AB、AC皆相切.下列四种作法中,哪一种是正确的
如图所示,已知△ABC中,AB<AC<BC.求作:一圆的圆心O,使得O在BC上,且圆O与AB、AC皆相切.下列四种作法中,哪一种是正确的
- A.作BC的中点O
- B.作∠A的平分线交BC于O点
- C.作AC的中垂线,交BC于O点
- D.自A点作一直线垂直BC,交BC于O点
B
分析:根据角平分线的性质,即角平分线上的点到角两边的距离相等,即可求解.
解答:根据角平分线上的点到角两边的距离相等,则
要使圆O与AB、AC都相切,只需作∠A的平分线交BC于O点.
故选B.
点评:本题较简单,考查的是角平分线的性质.
分析:根据角平分线的性质,即角平分线上的点到角两边的距离相等,即可求解.
解答:根据角平分线上的点到角两边的距离相等,则
要使圆O与AB、AC都相切,只需作∠A的平分线交BC于O点.
故选B.
点评:本题较简单,考查的是角平分线的性质.

练习册系列答案
相关题目
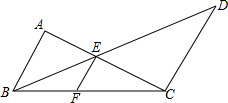 如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.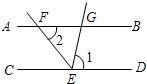 5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
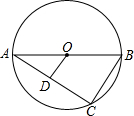 如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.
如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.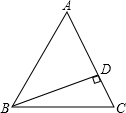 如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.
如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.