题目内容
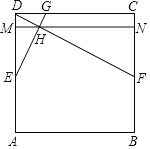
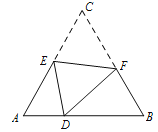
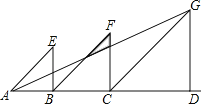
【题目】三个等腰直角三角形Rt△ABE,Rt△BCF,Rt△CDG如图摆放在射线AD上,直角顶点分别为B,C,D,已知相似比为2:3:4,AB=4,则(1)CG的长为_____;(2)图中阴影部分的面积是_____.
【答案】![]()
![]()
【解析】
(1)利用相似三角形对应边成比例列式计算即可得解;
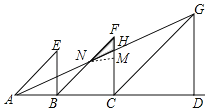
(2)如图,过点N作NM⊥CF,由平行线分线段成比例可求CH=![]() ,FH=CF﹣CH=
,FH=CF﹣CH=![]() ,通过证明△FNH∽△CGH,可得
,通过证明△FNH∽△CGH,可得![]() ,可求FN的长,由等腰直角三角形的性质可得MN的长,即可求解.
,可求FN的长,由等腰直角三角形的性质可得MN的长,即可求解.
解:(1)∵Rt△ABE,Rt△BCF,Rt△CDG都是等腰直角三角形,
∴Rt△ABE∽Rt△BCF∽Rt△CDG,
∴![]() ,且AB=4,
,且AB=4,
∴CD=8=DG,
∴CG=![]() CD=
CD=![]()
故答案为:![]() ;
;
(2)如图,过点N作NM⊥CF,
∵Rt△ABE∽Rt△BCF∽Rt△CDG,
∴![]() ,
,
∴BC=6,
∴CF=6,且CD=GD=8,AB=4
∴AC=10,AD=18,
∵CF∥GD,
∴![]() ,
,
∴![]()
∴CH=![]() ,
,
∴FH=CF﹣CH=![]() ,
,
∵∠FBC=∠GCD=45°,
∴FN∥CG,
∴△FNH∽△CGH,
∴![]() ,
,
∴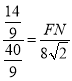 ,
,
∴FN=![]() ,
,
∴MN=![]() ,
,
∴阴影部分的面积=![]() ;
;
故答案为:![]() .
.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案【题目】某校为了解七、八年级学生英语听力训练情况(七、八年级学生人数相同),某周从这两个年级学生中分别随机抽查了30名同学,调查了他们周一至周五的听力训练情况,根据调查情况得到如下统计图表:
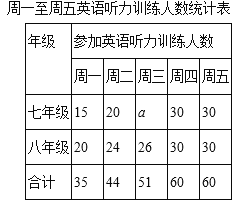

(1)填空:a= ;
(2)根据上述统计图表完成下表中的相关统计量:
年级 | 平均训练时间的中位数 | 参加英语听力训练人数的方差 |
七年级 | 24 | 34 |
八年级 |
| 14.4 |
(3)请你利用上述统计图表对七、八年级英语听力训练情况写出两条合理的评价;
(4)请你结合周一至周五英语听力训练人数统计表,估计该校七、八年级共480名学生中周一至周五平均每天有多少人进行英语听力训练.