题目内容
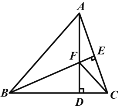
【题目】如图，在△ABC中，∠BAC＝90°，AB＝24，AC＝32，AD⊥BC，垂足为D，BC的垂直平分线分别交AC、BC于点E、F．求AD与EF的长．
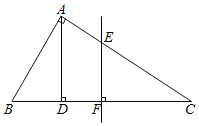
【答案】AD＝19.2，EF＝15
【解析】
连接BE，根据勾股定理求出BC，根据三角形的面积公式求出AD，根据线段垂直平分线的性质得到EB＝EC，BF＝FC＝20，根据勾股定理计算，得到答案．
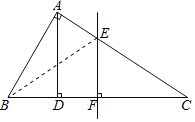
如图，连接BE，
由勾股定理得，BC＝
，
S△ABC＝
×AB×AC＝×BC×AD，即×24×32＝×40×AD，
解得，AD＝19.2，
∵EF是BC的垂直平分线，
∴EB＝EC，BF＝FC＝20，
∴AE＝32﹣EC＝32﹣EB，
在Rt△ABE中，BE2＝AB2+AE2，即BE2＝242+（32﹣EB）2，
解得，EB＝25，
则EF＝
，
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
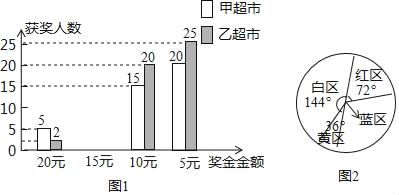
【题目】两家超市同时采取通过摇奖返现金搞促销活动，凡在超市购物满100元的顾客均可以参加摇奖一次．小明和小华对两家超市摇奖的50名顾客获奖情况进行了统计并制成了图表（如图）
奖金金额 获奖人数 | 20元 | 15元 | 10元 | 5元 |
商家甲超市 | 5 | 10 | 15 | 20 |
乙超市 | 2 | 3 | 20 | 25 |
（1）在甲超市摇奖的顾客获得奖金金额的中位数是 ，在乙超市摇奖的顾客获得奖金金额的众数是 ；
（2）请你补全统计图1；
（3）请你分别求出在甲、乙两超市参加摇奖的50名顾客平均获奖多少元？
（4）图2是甲超市的摇奖转盘，黄区20元、红区15元、蓝区10元、白区5元，如果你购物消费了100元后，参加一次摇奖，那么你获得奖金10元的概率是多少？
