题目内容
【题目】如图，平面直角坐标系中有点B(－2，0)和y轴上的动点A(0，a)，其中a>0，以点A为直角顶点在第二象限内作等腰直角三角形ABC，设点C的坐标为(c，d)．
（1）当a=4时，则点C的坐标为( ， )；
（2）动点A在运动的过程中，试判断c+d的值是否发生变化？若不变，请求出其值；若发生变化，请说明理由．
（3）当a=4时，在坐标平面内是否存在点P（不与点C重合），使△PAB与△ABC全等？若存在，求出点P的坐标；若不存在，请说明理由．
【答案】（1）﹣4，6；（2）c+d=2的值不变，值为2；（3）（﹣6，2）或（4，2）或（2，﹣2）．
【解析】
（1）先过点C作CE⊥y轴于E，证△AEC≌△BOA，推出CE=OA=4，AE=BO=2，即可得出点C的坐标；
（2）先过点C作CE⊥y轴于E，证△AEC≌△BOA，推出CE=OA=a，AE=BO=2，可得OE=a+2，即可得出点C的坐标为（﹣a，a+2），据此可得c+d的值不变；
（3）分为三种情况讨论，分别画出符合条件的图形，构造直角三角形，证出三角形全等，根据全等三角形对应边相等即可得出答案．
（1）如图1，过点C作CE⊥y轴于E，则∠CEA=∠AOB．
∵△ABC是等腰直角三角形，∴AC=BA，∠BAC=90°，∴∠ACE+∠CAE=90°=∠BAO+∠CAE，∴∠ACE=∠BAO．
在△ACE和△BAO中，∵
，∴△ACE≌△BAO（AAS），∴BO=AE，AO=CE．
∵B（﹣2，0），A（0，4），∴BO=AE=2，AO=CE=4，∴OE=4+2=6，∴C（﹣4，6）．
故答案为：﹣4，6；
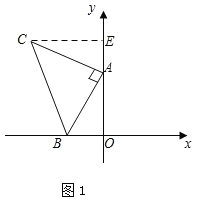
（2）动点A在运动的过程中，c+d=2的值不变，值为2．证明如下：
如图1，过点C作CE⊥y轴于E，则∠CEA=∠AOB．
∵△ABC是等腰直角三角形，∴AC=BA，∠BAC=90°，∴∠ACE+∠CAE=90°=∠BAO+∠CAE，∴∠ACE=∠BAO．
在△ACE和△BAO中，∵
，∴△ACE≌△BAO（AAS），∴BO=AE，AO=CE．
∵B（﹣2，0），A（0，a），∴BO=AE=2，AO=CE=a，∴OE=2+a，∴C（﹣a，2+a）．
又∵点C的坐标为（c，d），∴c+d=﹣a+2+a=2，即c+d=2，值不变；
（3）存在一点P，使△PAB与△ABC全等，分为三种情况：
①如图2，过P作PE⊥x轴于E，则∠PBA=∠AOB=∠PEB=90°，∴∠EPB+∠PBE=90°，∠PBE+∠ABO=90°，∴∠EPB=∠ABO．
在△PEB和△BOA中，∵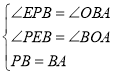
，∴△PEB≌△BOA（AAS），∴PE=BO=2，EB=AO=4，∴OE=2+4=6，即P的坐标是（﹣6，2）；
②如图3，过C作CM⊥x轴于M，过P作PE⊥x轴于E，则∠CMB=∠PEB=90°．
∵△CAB≌△PAB，∴∠PBA=∠CBA=45°，BC=BP，∴∠CBP=90°，∴∠MCB+∠CBM=90°，∠CBM+∠PBE=90°，∴∠MCB=∠PBE．
在△CMB和△BEP中，∵
，∴△CMB≌△BEP（AAS），∴PE=BM，CM=BE．
∵C（﹣4，6），B（﹣2，0），∴PE=2，OE=BE﹣BO=6﹣2=4，即P的坐标是（4，2）；
③如图4，过P作PE⊥x轴于E，则∠BEP=∠AOB=90°．
∵△CAB≌△PBA，∴AB=BP，∠CAB=∠ABP=90°，∴∠ABO+∠PBE=90°，∠PBE+∠BPE=90°，∴∠ABO=∠BPE．
在△BOA和△PEB中，∵
，∴△BOA≌△PEB（AAS），∴PE=BO=2，BE=OA=4，∴OE=BE﹣BO=4﹣2=2，即P的坐标是（2，﹣2）．
综合上述：符合条件的P的坐标是（﹣6，2）或（4，2）或（2，﹣2）．
