Question

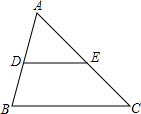
如图所示，在△ABC中，D、E、F分别是AB、AC、BC边的中点，连接DE、AF，添加一个条件______，使DE=AF；添加一个条件______，使DE⊥AF．

Answer 1

（1）在△ABC中，D、E、F分别是AB、AC、BC边的中点，则DF=

1

2

BC，
又因为在直角三角形中斜边中线为斜边边长的一半，
所以让△ABC为直角三角形，且BC为斜边即可，
所以添加条件∠BAC=90°，
故答案为∠BAC=90°

（2）因为DE为中位线，所以DE∥BC，
因此想让DE⊥AF，即让AF⊥BC即可．
在等腰三角形中斜边底边的中线垂直于底边，
所以当AB=AC时，DE⊥AF．
故答案为AB=AC．