��Ŀ����
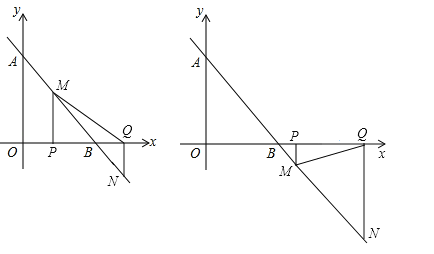
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��ͼ����y��������ύ�ڵ�A����x�ύ�ڵ�B��2��0������������ABO�����Ϊ2������P�ӵ�O��������ÿ��1����λ���ȵ��ٶ�������OB���˶�������Q��B��������x������������Pͬʱ����ͬ���ٶ��˶�����P��PM��X�ύֱ��AB��M��

��1����ֱ��AB�Ľ���ʽ��
��2������P���˶�ʱ������MPQ�����ΪS����P�˶���ʱ��Ϊt�룬��S��t�ĺ�����ϵʽ��ֱ��д���Ա�����ȡֵ��Χ����
��3������Q��QN��X�ύֱ��AB��N�����˶������У�P����B�غϣ����Ƿ����ijһʱ��t���룩��ʹ��MNQ�ǵ��������Σ������ڣ����ʱ��tֵ��
���𰸡���1��ֱ��AB�Ľ���ʽΪy=��x+2����2��t=![]() ��4ʱ����MNQ�ǵ��������Σ�
��4ʱ����MNQ�ǵ��������Σ�
�������������������1�����������ε�������OA����д����A�����꣬Ȼ�����ô���ϵ������һ�κ�������ʽ���
��2�����ݵ���ֱ�������ε����ʱ�ʾ��PM�������PQ�ij���Ȼ������ֱ�������ε������ʽ��ʽ�������ɵý⣻
��3����ʾ��PM��QN�������ù��ɶ�����ʽ��ʾ��QM2�������MN��Ȼ���MN=QN��MN=QM��QN=QM��������г�������⼴�ɣ�
����������⣺��1������B��2��0������OB=2����S��ABO=![]() OBOA=
OBOA=![]() ��2OA=2�����OA=2������A��0��2������ֱ��AB�Ľ���ʽΪy=kx+b������
��2OA=2�����OA=2������A��0��2������ֱ��AB�Ľ���ʽΪy=kx+b������ ![]() �������
������� ![]() ����ֱ��AB�Ľ���ʽΪy=��x+2��
����ֱ��AB�Ľ���ʽΪy=��x+2��
��2����OA=OB=2�����ABO�ǵ���ֱ�������Σ�����P��Q���ٶȶ���ÿ��1����λ���ȣ���PM=PB=OB��OP=2��t��PQ=OB=2�����MPQ�����ΪS=![]() PQPM=
PQPM=![]() ��2����2��t��=2��t������P���߶�OB���˶�����0��t��2����S��t�ĺ�����ϵʽΪS=2��t��0��t��2����
��2����2��t��=2��t������P���߶�OB���˶�����0��t��2����S��t�ĺ�����ϵʽΪS=2��t��0��t��2����
��3��t��ʱ��PM=PB=|2��t|��QN=BQ=t�����ԣ�QM2=PM2+PQ2=��2��t��2+4��MN=![]() ��QN��PM��=
��QN��PM��=![]() ��t��t��2��=
��t��t��2��=![]() ��
��
����MN=QN����t=![]() ��
��
����MN=QM����2��t��2+4=��![]() ��2�������ã�t2��4t=0�����t1=0����ȥ����t2=4��
��2�������ã�t2��4t=0�����t1=0����ȥ����t2=4��
����QN=QM����2��t��2+4=t2�����ã�4t��8=0�����t=2����ʱ��P�����B�غϣ�����������ȥ��
����������t=![]() ��4ʱ����MNQ�ǵ��������Σ�
��4ʱ����MNQ�ǵ��������Σ�