题目内容
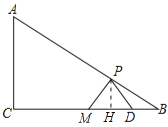
【题目】如图在△ABC中,∠C=90°,AC=6,BC=8,M是BC的中点,P为AB上的一个动点(不可以与A,B重合),并作∠MPD=90°,PD交BC(或BC的延长线)于点D
(1)记BP的长为x,△BPM的面积为y,求y与x的函数关系式,并写出自变量x的取值范围。
(2)是否存在这样的点P,使得△MPD与△ABC相似?若存在,请求出x的值;若不存在,请说明理由

【答案】(1) y=![]() x(0<x<10 且x≠5);(2) 存在符合条件的P点,且x=2 .5或3.2
x(0<x<10 且x≠5);(2) 存在符合条件的P点,且x=2 .5或3.2
【解析】试题分析:(1)△BMP中,BM的长易求得,关键是求BM边上的高;过P作PH⊥BC于H,易证得△BPH∽△BAC,通过相似三角形得出的成比例线段可求出PH的长,进而可求出y、x的函数关系式;
(2)所求的两个三角形中,已知∠MPD=∠ACB=90°,若使两三角形相似要分两种情况进行讨论;
一、D在BC上,
①∠PMB=∠B,此时PM=BM,MH=BH=2,可根据相似三角形得出的成比例线段求出x的值;②∠PMB=∠A,此时△BPM∽△BCA,同①可求得x的值;
二、D在BC延长线上时;
由于∠PMD>∠B,因此只有一种情况:∠PMD=∠BAC;当P、A重合时,易证得∠MAC=∠PDM,由于tan∠MAC=![]() <tan∠B,所有∠MAC<∠B,即当D在BC延长线上时,∠PDM总小于∠B,所有△PDM和△ABC不会相似;
<tan∠B,所有∠MAC<∠B,即当D在BC延长线上时,∠PDM总小于∠B,所有△PDM和△ABC不会相似;
综合两种情况,可得出符合条件的x的值.
试题解析:(1)过P作PH⊥BC于H,则PH∥AC;
Rt△ABC中,AC=6,BC=8;则AB=10.
∵P为AB上动点可与A、B重合(与A重合BP为0,与B重合BP为10)
但是x不能等于5.
∵当x=5时,P为AB中点,PM∥AC,得到PD∥BC,PD与BC无交点,与题目已知矛盾,所以x的取值范围是,0≤x≤![]() 或5<x≤10,
或5<x≤10,
易知△BPH∽△BAC,得:![]() ,PH=
,PH=![]() x;
x;
∴y=![]() ×4×
×4×![]() x=
x=![]() x(0≤x≤
x(0≤x≤![]() 或5<x≤10);
或5<x≤10);
(2)当D在BC上时,
①∠PMB=∠B时,BP=PM,MH=BH=2;
PB=x,AB=10,MH=2,BC=8,
此时△PBH∽△BCA,
∴![]() ,得:
,得:![]() ,解得x=
,解得x=![]() ;
;
②∠PMB=∠A时,△DPM∽△BCA,得:![]() ,即DPBA=DMBC;
,即DPBA=DMBC;
∴10x=4×8,解得x=![]() ;
;
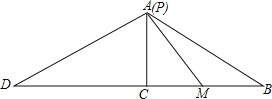
当D在BC延长线上时,
由于∠PMD>∠B,所以只讨论∠PDM=∠B的情况;
当P、A重合时,Rt△MPD中,AC⊥MD,则∠MAC=∠PDM,
∵tan∠MAC=![]() ,tanB=
,tanB=![]() ,tan∠MAC<tanB,
,tan∠MAC<tanB,
∴∠MAC<∠B,即∠PDM<∠B;
由于当P、A重合时,∠PDM最大,故当D在BC延长线上时,∠B>∠PDM;
所以△PDM和△ACB不可能相似;
综上所述,存在符合条件的P点,且x=2.5或3.2.

 口算能手系列答案
口算能手系列答案