题目内容
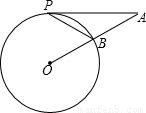
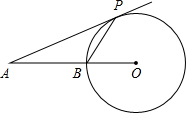 如图,AP为⊙O切线,P为切点,OA交⊙O于点B,∠A=40°,则∠APB=
如图,AP为⊙O切线,P为切点,OA交⊙O于点B,∠A=40°,则∠APB=
- A.25°
- B.20°
- C.40°
- D.35°
A
分析:连接OP,得到PO垂直PA.通过三角形的内角和定理求出∠O的度数,从而得到∠OPB=65°,进而得到∠APB=25°.
解答: 解:连OP,如图,
解:连OP,如图,
∵AP为⊙O切线,
∴OP⊥AP,
∵∠A=40°,
∴∠O=50°,
∴∠1=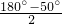 =65°,
=65°,
∴∠APB=90°-65°=25°.
故选A.
点评:熟练掌握切线的性质.通常我们把圆的切线问题转化为垂直问题,因此连接圆心和切点是常作的辅助线.
分析:连接OP,得到PO垂直PA.通过三角形的内角和定理求出∠O的度数,从而得到∠OPB=65°,进而得到∠APB=25°.
解答:
 解:连OP,如图,
解:连OP,如图,∵AP为⊙O切线,
∴OP⊥AP,
∵∠A=40°,
∴∠O=50°,
∴∠1=
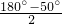 =65°,
=65°,∴∠APB=90°-65°=25°.
故选A.
点评:熟练掌握切线的性质.通常我们把圆的切线问题转化为垂直问题,因此连接圆心和切点是常作的辅助线.

练习册系列答案
相关题目
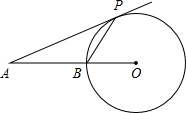 如图,AP为⊙O切线,P为切点,OA交⊙O于点B,∠A=40°,则∠APB=( )
如图,AP为⊙O切线,P为切点,OA交⊙O于点B,∠A=40°,则∠APB=( )| A、25° | B、20° | C、40° | D、35° |
 9、如图,AP为圆O的切线,P为切点,OA交圆O于点B,若∠A=40°,则∠APB等于( )
9、如图,AP为圆O的切线,P为切点,OA交圆O于点B,若∠A=40°,则∠APB等于( )