题目内容

9、如图，AP为圆O的切线，P为切点，OA交圆O于点B，若∠A=40°，则∠APB等于（　　）
分析：如图，连接OP，由于AP为圆O的切线可以得到∠OPA=90°，由此可以求出∠O的度数；又由OB=OP可以求出∠OPB=∠OBP的度数，然后即可求出∠APB的度数．
解答：解：如图，连接OP，
∵AP为圆O的切线，P为切点，
∴∠OPA=90°，
∴∠O=90°-∠A=50°，
∵OB=OP，
∴∠OPB=∠OBP=（180°-∠O）÷2=65°，
∴∠APB=90°-∠OPB=25°．
故选A．
点评：本题利用了切线的性质，直角三角形的性质，等边对等角，三角形内角和定理求解，综合性比较强．
练习册系列答案
相关题目
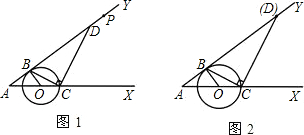如图1，已知O是锐角∠XAY的边AX上的动点，以点O为圆心、R为半径的圆与射线AY切于点B，交射线OX于点C，连接BC，作CD⊥BC精英家教网，交AY于点D．
（1）求证：△ABC∽△ACD；
（2）若P是AY上一点，AP=4，且sinA=
35
，
①如图2，当点D与点P重合时，求R的值；
②当点D与点P不重合时，试求PD的长（用R表示）．
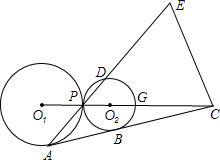如图1，在直角梯形ABCD中，AD∥BC，∠C=90°，BC=12，AD=18，AB=10．动点P、Q分别从点D、B同时出发，动点P沿射线DA的方向以每秒2个单位长的速度运动，动点Q在线段BC上以每秒1个单位长的速度向点C运动，当点Q运动到点精英家教网C时，点P随之停止运动．设运动的时间为t（秒）．
（1）当点P在线段DA上运动时，连接BD，若∠ABP=∠ADB，求t的值；
（2）当点P在线段DA上运动时，若以BQ为直径的圆与以AP为直径的圆外切，求t的值；
（3）设射线PQ与射线AB相交于点E，△AEP能否为等腰三角形？如果能，请直接写出t的值；如果不能，请说明理由．
如图，⊙O1与⊙O2外切于点P，AB是两圆外公切线，A、B为切点，AB与O1O2的延长线交于C点，在AP延精英家教网长线上有一点E，满足
AP
AB
=
AC
AE
，PE交⊙O2于D．
（1）求证：AC⊥EC；
（2）求证：PC=EC；
（3）若AP=4，PD=
9
4
，求
BC
EC
的值．
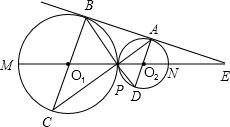如图，已知⊙O1和⊙O2外切于点P，AB是两圆的外公切线，A，B为切点，AP的延精英家教网长线交⊙O1于C点，BP的延长线交⊙O2于D点，直线O1O2交⊙O1于M，交⊙O2于N，与BA的延长线交于点E．
求证：（1）AB2=BC•DA．
（2）线段BC，AD分别是两圆的直径．
（3）PE2=BE•AE．
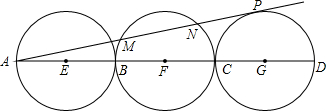如图，已知AD=30，点B，C是AD上的三等分点，分别以AB，BC，CD为直径作圆，圆心分别为E，F，G，AP切⊙G于点P，交⊙F于M，N，求弦MN的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网