��Ŀ����
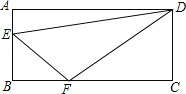
����Ŀ����ͼ��ʾ����ƽ���ı���ABCD�У���A=90����AB=6cm��BC=12cm����E�ɵ�A������AB�������B�����ƶ����ٶ�Ϊ1cm/s����F�ɵ�B������BC�������C�����ƶ����ٶ�Ϊ2cm/s���������E��Fͬʱ��A��B�������������EF�������˶�ʱ��Ϊts������������⣮
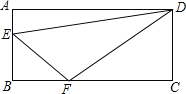
��1����tΪ ʱ����BEFΪ����ֱ�������Σ�
��2����tΪ ʱ����DFCΪ����ֱ�������Σ�
��3���Ƿ����ijһʱ�̣�ʹ��EFB�ס�FDC�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��2s����2��3s����3����t=1.5ʱ����EFB�ס�FDC��
��������
�����������1������֪������֤�ı���ABCD�Ǿ��Σ�������A=��B=��C=90��������BEFΪ����ֱ�������Σ���BE=BF�����������t��ֵ��
��2���ɣ�1����֪��C=90��������DFCΪ����ֱ�������Σ���CF=DC�����������t��ֵ��
��3������EFB�ס�FDC����BE��CF=BF��DC�������Ŀ����֪�����ɵõ�����t�ķ��̣��ⷽ�̼��ɵ�֪�Ƿ����t��ֵ��
�⣺
��1������ƽ���ı���ABCD�У���A=90����
���ı���ABCD�Ǿ��Σ�
���A=��B=��C=90����
������BEFΪ����ֱ�������Σ���BE=BF��
����E�ɵ�A������AB�������B�����ƶ����ٶ�Ϊ1cm/s����F�ɵ�B������BC�������C�����ƶ����ٶ�Ϊ2cm/s��AB=6cm��BC=12cm��
��BE=��6��t��cm��BF=2t��
��6��t=2t��
��t=2s��
�ʴ�Ϊ2s��
��2���ɣ�1����֪����DFCΪ����ֱ�������Σ���CF=DC��
��CF=2tcm��DC=6cm��
��2t=6��
��t=3s��
�ʴ�Ϊ3s��
��3������ijһʱ�̣�ʹ��EFB�ס�FDC��
�ߡ�EFB�ס�FDC��
��BE��CF=BF��DC��
��![]() ��
��
�����ã�2t2��15t+18=0��
����2t��3����t��6��=0��
��ã�t=1.5��t=6���ᣩ��
����t=1.5ʱ����EFB�ס�FDC��