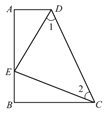
题目内容
【题目】我们定义:在一个图形上画一条直线,若这条直线既平分该图形的面积,又平分该图形的周长,我们称这条直线为这个图形的“等分积周线”.
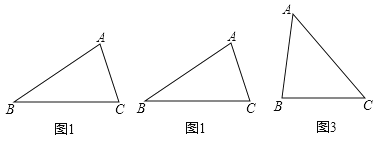
(1)如图1,在△ABC中,AB=BC,且BC≠AC,请你在图1中用尺规作图作出△ABC的一条“等分积周线”;
(2)在图1中,过点C能否画出一条“等分积周线”?若能,说出确定的方法;若不能,请说明理由.
(3)如图3,在△ABC中,AB=BC=6cm,AC=8cm,请你不过△ABC的顶点,画出△ABC的一条“等分积周线”,并说明理由.
【答案】(1)作图见解析;
(2)不能,理由见解析;
(3)作图见解析,理由见解析.
【解析】(1)作线段AC的中垂线BD即可得出答案;(2)若直线CD平分△ABC的面积,那么S△ADC=S△DBC,得出AC≠BC,进而得出答案;(3)在AC上取一点F,使得FC=AB=6,在BC上取一点E,使得BE=2,作直线EF,则EF是△ABC的等分积周线,结合全等三角形的判定与性质得出答案.
解:
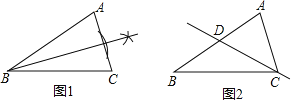
(1)如图1所示:作线段AC的中垂线BD或∠B的平分线即可;
(2)不能,理由:如图2,若直线CD平分△ABC的面积,那么S△ADC=S△DBC,
∴AD=BD,
∵AC≠BC,
∴AD+AC≠BD+BC,
∴过点C不能画出一条“等分积周线”
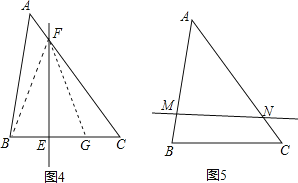
(3)如图4,在AC上取一点F,使得FC=AB=6,在BC上取一点E,使得BE=2,
作直线EF,则EF是△ABC的等分积周线,
理由:由作图可得:AF=AC-FC=8-6=2,在CB上取一点G,使得CG=AF=2,则有AB+AF=CF+CG,
∵AB=BC,
∴∠A=∠C,
在△ABF和△CFG中
∴△ABF≌△CFG(SAS),
∴S△ABF=S△CFG,
又易得BE=EG=2,
∴S△BFE=S△EFG,
∴S△EFC=S四边形ABEF,
AF+AB+BE=CE+CF=10,
∴EF是△ABC的等分积周线,
若如图5,当BM=2cm,AN=6cm时,直线MN也是△ABC的等分积周线.(其实是同一条),
另外本问的说理也可以通过作高,进行相关计算说明).
“点睛”此题主要考查了应用与设计作图和全等三角形的判定与性质和勾股定理等知识,根据题意正确分割图形是解题关键.