题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=BC , BE⊥CE于点E . AD⊥CE于点D.求证:△BEC≌△CDA.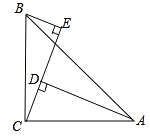
【答案】证明:∵BE⊥CE于E , AD⊥CE于D , ∴∠BEC=∠CDE=90°,在Rt△BEC中,∠BCE+∠CBE=90°,在Rt△BCA中,∠BCE+∠ACD=90°,∴∠CBE=∠ACD , 在△BEC和△CDA中,∠BEC=∠CDA , ∠CBE=∠ACD , BC=AC , ∴△BEC≌△CDA(AAS) .
【解析】证明:∵BE⊥CE于E , AD⊥CE于D , ∴∠BEC=∠CDE=90°,在Rt△BEC中,∠BCE+∠CBE=90° , 在Rt△BCA中 , ∠BCE+∠ACD=90° , ∴∠CBE=∠ACD ,
在△BEC和△CDA中,∠BEC=∠CDA , ∠CBE=∠ACD , BC=AC , ∴△BEC≌△CDA(AAS) .

练习册系列答案
相关题目