题目内容
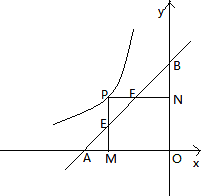
已知如图,动点P在反比例函数y=- (x<0)的图象上运动,点A点B分别在X轴,Y轴上,且OA=
(x<0)的图象上运动,点A点B分别在X轴,Y轴上,且OA=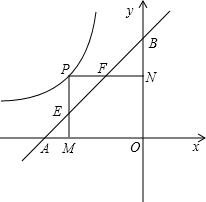 OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;
OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;
(1)当点P的纵坐标为 时,连OE,OF,求E、F两点的坐标及△EOF的面积;
时,连OE,OF,求E、F两点的坐标及△EOF的面积;
(2)动点P在函数 y=- (x<0)的图象上移动,它的坐标设为P(a,b) (-2<a<0,0<b<2且|a|≠|b|),其他条件不变,探索:以AE、EF、BF为边的三角形是怎样的三角形?并证明你的结论.
(x<0)的图象上移动,它的坐标设为P(a,b) (-2<a<0,0<b<2且|a|≠|b|),其他条件不变,探索:以AE、EF、BF为边的三角形是怎样的三角形?并证明你的结论.
解:(1)由条件知A(-2,0),B(0,2),易求得直线AB的解析式为:y=x+2
又∵点P在函数y=- 上,且纵坐标为
上,且纵坐标为 ,
,
∴P(- ,
, )
)
把x=- 代入y=x+2中得y=
代入y=x+2中得y= ,
,
∴E(- ,
, )
)
把y= 代入y=x+2中得x=-
代入y=x+2中得x=-
∴F(- ,
, )
)
S△E0F=S△AOF-S△AOE= ×|-2|×
×|-2|× -
- ×|-2|×
×|-2|× =
=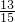 ;
;
(2)以AE,BF,EF为边的三角形是直角三角形.
理由如下:
由条件知△AOB是等腰直角三角形,则△AME,△EPF,△FNB均为等腰直角三角形,又-2<a<0,0<b<2
AM=2-(-a)=2+a
∴AE2=( AM)2=2a2+8a+8
AM)2=2a2+8a+8
BN=2-b
∴BF2=( BN)2=2b2-8b+8
BN)2=2b2-8b+8
PE=PM-EN=PM-AM=b-(2+a)=b-a-2 而ab=-2
∴EF2=( PE)2=2a2+2b2+8a-8b+16
PE)2=2a2+2b2+8a-8b+16
又|a|≠|b|
∴AE≠BF
而(2a2+8a+8)+(2b2-8b+8)=2a2+2b2+8a-8b+16
∴AE2+BF2=EF2
故以AE,BF,EF为边的三角形是直角三角形.
分析:(1)分别求得点P、点E、点F的坐标,然后即可求得三角形EOF的面积;
(2)由条件知△AOB是等腰直角三角形,则△AME,△EPF,△FNB均为等腰直角三角形,然后表示出AE2、BF2、EF2=( PE)2得到AE2+BF2=EF2,利用勾股定理即可判定直角三角形.
PE)2得到AE2+BF2=EF2,利用勾股定理即可判定直角三角形.
点评:本题考查了反比例函数的综合知识,解题的关键是利用反比例函数的性质、特点求得相应的点的坐标.
又∵点P在函数y=-
 上,且纵坐标为
上,且纵坐标为 ,
,∴P(-
 ,
, )
)把x=-
 代入y=x+2中得y=
代入y=x+2中得y= ,
,∴E(-
 ,
, )
)把y=
 代入y=x+2中得x=-
代入y=x+2中得x=-
∴F(-
 ,
, )
)S△E0F=S△AOF-S△AOE=
 ×|-2|×
×|-2|× -
- ×|-2|×
×|-2|× =
=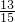 ;
;(2)以AE,BF,EF为边的三角形是直角三角形.
理由如下:
由条件知△AOB是等腰直角三角形,则△AME,△EPF,△FNB均为等腰直角三角形,又-2<a<0,0<b<2
AM=2-(-a)=2+a
∴AE2=(
 AM)2=2a2+8a+8
AM)2=2a2+8a+8BN=2-b
∴BF2=(
 BN)2=2b2-8b+8
BN)2=2b2-8b+8PE=PM-EN=PM-AM=b-(2+a)=b-a-2 而ab=-2
∴EF2=(
 PE)2=2a2+2b2+8a-8b+16
PE)2=2a2+2b2+8a-8b+16又|a|≠|b|
∴AE≠BF
而(2a2+8a+8)+(2b2-8b+8)=2a2+2b2+8a-8b+16
∴AE2+BF2=EF2
故以AE,BF,EF为边的三角形是直角三角形.
分析:(1)分别求得点P、点E、点F的坐标,然后即可求得三角形EOF的面积;
(2)由条件知△AOB是等腰直角三角形,则△AME,△EPF,△FNB均为等腰直角三角形,然后表示出AE2、BF2、EF2=(
 PE)2得到AE2+BF2=EF2,利用勾股定理即可判定直角三角形.
PE)2得到AE2+BF2=EF2,利用勾股定理即可判定直角三角形.点评:本题考查了反比例函数的综合知识,解题的关键是利用反比例函数的性质、特点求得相应的点的坐标.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
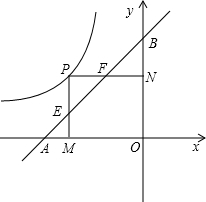 OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;
OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;
 如图,已知一次函数y=ax+b(a≠0)的图象与反比例函数
如图,已知一次函数y=ax+b(a≠0)的图象与反比例函数