��Ŀ����
��֪��ͼ������P�ڷ���������y=-| 2 |
| x |
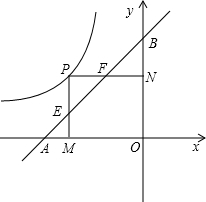 OB=2��PM��X����M����AB�ڵ�E��PN��Y���ڵ�N����AB��F��
OB=2��PM��X����M����AB�ڵ�E��PN��Y���ڵ�N����AB��F����1������P��������Ϊ
| 5 |
| 3 |
��2������P�ں��� y=-
| 2 |
| x |
��������1���ֱ���õ�P����E����F�����꣬Ȼ�����������EOF�������
��2��������֪��AOB�ǵ���ֱ�������Σ����AME����EPF����FNB��Ϊ����ֱ�������Σ�Ȼ���ʾ��AE2��BF2��EF2=��
PE��2�õ�AE2+BF2=EF2�����ù��ɶ��������ж�ֱ�������Σ�
��2��������֪��AOB�ǵ���ֱ�������Σ����AME����EPF����FNB��Ϊ����ֱ�������Σ�Ȼ���ʾ��AE2��BF2��EF2=��
| 2 |
����⣺��1��������֪A��-2��0����B��0��2���������ֱ��AB�Ľ���ʽΪ��y=x+2
�֡ߵ�P�ں���y=-
�ϣ���������Ϊ
��
��P��-
��
��
��x=-
����y=x+2�е�y=
��
��E��-
��
��
��y=
����y=x+2�е�x=-
��F��-
��
��
S��E0F=S��AOF-S��AOE=
��|-2|��
-
��|-2|��
=
��
��2����AE��BF��EFΪ�ߵ���������ֱ�������Σ�
�������£�
������֪��AOB�ǵ���ֱ�������Σ����AME����EPF����FNB��Ϊ����ֱ�������Σ���-2��a��0��0��b��2
AM=2-��-a��=2+a
��AE2=��
AM��2=2a2+8a+8
BN=2-b
��BF2=��
BN��2=2b2-8b+8
PE=PM-EN=PM-AM=b-��2+a��=b-a-2 ��ab=-2
��EF2=��
PE��2=2a2+2b2+8a-8b+16
��|a|��|b|
��AE��BF
����2a2+8a+8��+��2b2-8b+8��=2a2+2b2+8a-8b+16
��AE2+BF2=EF2
����AE��BF��EFΪ�ߵ���������ֱ�������Σ�
�֡ߵ�P�ں���y=-
| 2 |
| x |
| 5 |
| 3 |
��P��-
| 6 |
| 5 |
| 5 |
| 3 |
��x=-
| 6 |
| 5 |
| 4 |
| 5 |
��E��-
| 6 |
| 5 |
| 4 |
| 5 |
��y=
| 5 |
| 3 |
| 1 |
| 3 |
��F��-
| 1 |
| 3 |
| 5 |
| 3 |
S��E0F=S��AOF-S��AOE=
| 1 |
| 2 |
| 5 |
| 3 |
| 1 |
| 2 |
| 4 |
| 5 |
| 13 |
| 15 |
��2����AE��BF��EFΪ�ߵ���������ֱ�������Σ�
�������£�
������֪��AOB�ǵ���ֱ�������Σ����AME����EPF����FNB��Ϊ����ֱ�������Σ���-2��a��0��0��b��2
AM=2-��-a��=2+a
��AE2=��
| 2 |
BN=2-b
��BF2=��
| 2 |
PE=PM-EN=PM-AM=b-��2+a��=b-a-2 ��ab=-2
��EF2=��
| 2 |
��|a|��|b|
��AE��BF
����2a2+8a+8��+��2b2-8b+8��=2a2+2b2+8a-8b+16
��AE2+BF2=EF2
����AE��BF��EFΪ�ߵ���������ֱ�������Σ�
���������⿼���˷������������ۺ�֪ʶ������Ĺؼ������÷��������������ʡ��ص������Ӧ�ĵ�����꣮

��ϰ��ϵ�д�
�����Ŀ
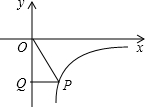 ��ͼ������P�ڷ���������
��ͼ������P�ڷ���������
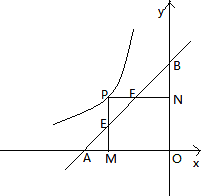
 ��x��0����ͼ�����˶�����A��B�ֱ���X�ᣬY���ϣ���OA=
��x��0����ͼ�����˶�����A��B�ֱ���X�ᣬY���ϣ���OA=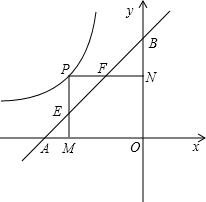 OB=2��PM��X����M����AB�ڵ�E��PN��Y���ڵ�N����AB��F��
OB=2��PM��X����M����AB�ڵ�E��PN��Y���ڵ�N����AB��F�� ʱ����OE��OF����E��F��������꼰��EOF�������
ʱ����OE��OF����E��F��������꼰��EOF�������