题目内容
如图1,已知两个反比例函数y1=
和y2=
(k1>k2>0)在平面直角坐标系xOy第一象限内的图象如图所示,动点A在y1=
的图象上,AB∥y轴,与y2=
的图象交于点B,AC、BD都与x轴平行,分别与y2=
、y1=
的图象交于点C、D.
(1)用含k1、k2的代数式表示四边形ACOB的面积.
(2)当k1=8,k2=2时,
①若点A横坐标为2,求梯形ACBD的对角线的交点F的坐标;
②将y2=
沿x轴翻折得到y3=
,动点N在y3上,若∠AON=90°,求
的值.

| k1 |
| x |
| k2 |
| x |
| k1 |
| x |
| k2 |
| x |
| k2 |
| x |
| k1 |
| x |
(1)用含k1、k2的代数式表示四边形ACOB的面积.
(2)当k1=8,k2=2时,
①若点A横坐标为2,求梯形ACBD的对角线的交点F的坐标;
②将y2=
| k2 |
| x |
| k3 |
| x |
| AO |
| ON |

分析:(1)直接根据反比例函数系数k的几何意义进行解答即可;
(2)①首先根据点A的横坐标和双曲线的解析式,可以分别求得点A、B、C、D四个点的坐标.根据点C、D的坐标可以运用待定系数法求得直线CD的解析式,根据题意,得点F的横坐标是2,再进一步把x=2代入直线CD的解析式即可求得点F的纵坐标;
②先根据关于x轴对称的点的坐标特点求出反比例函数y3=
的解析式,设出N点坐标,根据互相垂直的两条直线的关系求出N点坐标,再根据勾股定理求出AO及ON的长,故可得出结论.
(2)①首先根据点A的横坐标和双曲线的解析式,可以分别求得点A、B、C、D四个点的坐标.根据点C、D的坐标可以运用待定系数法求得直线CD的解析式,根据题意,得点F的横坐标是2,再进一步把x=2代入直线CD的解析式即可求得点F的纵坐标;
②先根据关于x轴对称的点的坐标特点求出反比例函数y3=
| k3 |
| x |
解答:解:(1)∵点A、B分别在反比例函数y1=
,y2=
,的图象上,AG⊥x轴,AH⊥y轴,
∴S矩形AHOG=k1,S△HOC=S△BOG=
∴S四边形ACOB=S矩形AHOG-(S△HOC+S△BOG=)=k1-2×
=k1-k2;
 (2)①由题可知,当点A的横坐标为2时,点A、B、C、D的坐标分别为A(2,4),B(2,1),C(
(2)①由题可知,当点A的横坐标为2时,点A、B、C、D的坐标分别为A(2,4),B(2,1),C(
,4),D(8,1).
∵设直线CD的解析式为y=kx+b,
∴
,解得
,
∴直线CD的解析式为y=-
x+
,
∵AB∥y轴,F为梯形ACBD的对角线的交点,
∴x=2时,y=(-
)×2+
=
∴点F的坐标为(2,
)
②∵反比例函数y2=
与y3=
关于x轴对称,
∴反比例函y3=
的解析式为y=-
,
∵点N在反比例函数y=-
的图象上,
∴设N(x,-
)(x>0),
∵∠AON=90°,由①知A(2,4),
∴
×(-
)=-1,解得x=2或x=-2(舍去),
∴N(2,-1),
∴ON=
=
,AO=
=2
,
∴
=
=2.
| k1 |
| x |
| k2 |
| x |
∴S矩形AHOG=k1,S△HOC=S△BOG=
| k2 |
| 2 |
∴S四边形ACOB=S矩形AHOG-(S△HOC+S△BOG=)=k1-2×
| k2 |
| 2 |
 (2)①由题可知,当点A的横坐标为2时,点A、B、C、D的坐标分别为A(2,4),B(2,1),C(
(2)①由题可知,当点A的横坐标为2时,点A、B、C、D的坐标分别为A(2,4),B(2,1),C(| 1 |
| 2 |
∵设直线CD的解析式为y=kx+b,
∴
|
|
∴直线CD的解析式为y=-
| 2 |
| 5 |
| 21 |
| 5 |
∵AB∥y轴,F为梯形ACBD的对角线的交点,
∴x=2时,y=(-
| 2 |
| 5 |
| 21 |
| 5 |
| 17 |
| 5 |
∴点F的坐标为(2,
| 17 |
| 5 |
②∵反比例函数y2=
| k2 |
| x |
| k3 |
| x |
∴反比例函y3=
| k3 |
| x |
| 2 |
| x |
∵点N在反比例函数y=-
| 2 |
| x |
∴设N(x,-
| 2 |
| x |
∵∠AON=90°,由①知A(2,4),
∴
| 4 |
| 2 |
| ||
| x |
∴N(2,-1),
∴ON=
| 22+12 |
| 5 |
| 22+42 |
| 5 |
∴
| AO |
| ON |
2
| ||
|
点评:本题考查的是反比例函数综合题,涉及到反比例函数系数k的几何意义、用待定系数法求一次函数函数的解析式及关于x轴对称的点的坐标特点,涉及面较广,难度适中.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比列函数
如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比列函数 如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比列函数
如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比列函数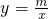 的图象的两个交点.
的图象的两个交点.