题目内容
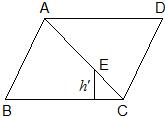13、如图：平行四边形ABCD中，BC边上的高等于h，点E是对角线AC上靠近点C的三等分点，它到BC边上的距离等于h′，则h′：h=1：3
．分析：作辅助线：AG⊥BC，EF⊥BC．则可知△CEF∽△CAG，然后求出相似比即可．
解答：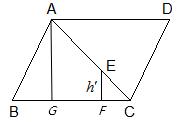
解：过点A做AG⊥BC于点G，那么AD=h
设EF⊥BC于点F
∴EF∥AG
∴△CEF∽△CAG
∴h′：h=CE：AC=1：3．
解：过点A做AG⊥BC于点G，那么AD=h设EF⊥BC于点F
∴EF∥AG
∴△CEF∽△CAG
∴h′：h=CE：AC=1：3．
点评：题中已有一垂直，可做一垂直，构造相似三角形，利用相似三角形的性质求解．
练习册系列答案
相关题目
次方程x2-7x+12=0的两个根，且OA＞OB．
10、如图，平行四边形ABCD中，∠ABC的角平分线BE交AD于E点，AB=3，ED=1，则平行四边形ABCD的周长是
如图，平行四边形ABCD中，对角线AC和BD相交于点O，如果AC=12，BD=10，AB=m，那么m的取值范围是
如图，平行四边形ABCD的两条对角线AC、BD相交于点O，AB=5，AC=6，DB=8，则四边形ABCD是的周长为