题目内容
如图，已知∠ACD=135°，∠DFA=132°，∠A=32°，求∠D的度数．
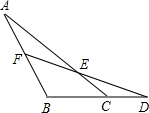
∵∠AEF+（∠A+∠AFE）=180°，
∠DEC+（∠D+∠DCE）=180°，
∴∠A+∠AFE=180°-∠AFE，
∠D+∠DCE=180°-∠DEC，
又∵∠AEF=∠DEC，
∴∠A+∠AFE=∠D+∠DCE，
∴∠D=∠A+∠AFE-∠DCE=32°+132°-135°=29°．
答：∠D为29°．
∠DEC+（∠D+∠DCE）=180°，
∴∠A+∠AFE=180°-∠AFE，
∠D+∠DCE=180°-∠DEC，
又∵∠AEF=∠DEC，
∴∠A+∠AFE=∠D+∠DCE，
∴∠D=∠A+∠AFE-∠DCE=32°+132°-135°=29°．
答：∠D为29°．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
